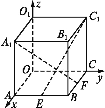
[题目]在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是AB,BC上的动点,且AE=BF,求证:A1F⊥C1E. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是AB,BC上的动点,且AE=BF,求证:A1F⊥C1E.

【答案】见解析

【解析】

以O为坐标原点建立如图所示的空间直角坐标系,则A1(a,0,a),C1(0,a,a).

设AE=BF=x,则E(a,x,0),F(a-x,a,0)，所以=(-x,a,-a),=(a,x-a,-a).

则计算即可.

证明：以O为坐标原点建立如图所示的空间直角坐标系,则A1(a,0,a),C1(0,a,a).

设AE=BF=x,则E(a,x,0),F(a-x,a,0)，所以=(-x,a,-a),=(a,x-a,-a).

因为=(-x,a,-a)·(a,x-a,-a)=-ax+ax-a2+a2=0,所以,即A1F⊥C1E.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

【题目】设点F1（﹣c，0），F2（c，0）分别是椭圆C： =1（a＞1）的左、右焦点，P为椭圆C上任意一点，且的最小值为0．

（1）求椭圆C的方程；
（2）如图，动直线l：y=kx+m与椭圆C有且仅有一个公共点，点M，N是直线l上的两点，且F1M⊥l，F2N⊥l，求四边形F1MNF2面积S的最大值．

【题目】在△ABC中，∠A=60°，AB=3，AC=2．若 =2 ， =λ ﹣ （λ∈R），且 =﹣4，则λ的值为．

【题目】已知函数f（x）= x3﹣ ax2 ， a∈R，
（1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；
（2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．

【题目】在正方体ABCD—A1B1C1D1中，若E为A1C1中点，则直线CE垂直于（）

A. AC B. BD C. A1D D. A1A

【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30），[30，40），…[80，90]，并整理得到如下频率分布直方图：

（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．