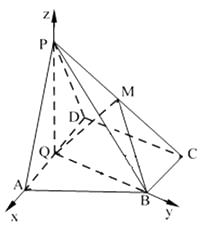
题目内容
【题目】如图,在四棱锥 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点,
的中点, ![]() 是棱
是棱 ![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面 ![]() 底面
底面 ![]() ;
;
(2)设 ![]() ,若二面角
,若二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,试确定
,试确定 ![]() 的值.
的值.
【答案】
(1)
证明:∵AD//BC,BC= ![]() ,Q是AD的中点,
,Q是AD的中点,
∴BC ![]() DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
∵AD⊥CD,∴QB⊥AD.
∵PA=PD=2,AD=2,Q是AD的中点,∴ ![]()
又∵QB=CD= ![]() ,
, ![]()
∴ ![]() ,即PQ⊥QB,又PQ
,即PQ⊥QB,又PQ ![]() AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
(2)
解:∵PA=PD=2,Q是AD的中点,∴PQ⊥AD.∵平面PAD⊥平面ABCD,且平面PAD ![]() 平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
则平面BQC的法向量为 ![]()
设 ![]() ,则
,则 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]()
则 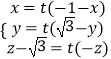 ,即
,即 ![]() ,
, ![]() ,
, ![]() ,在平面MBQ中,
,在平面MBQ中, ![]() ,
, ![]() ,设平面MBQ的法向量为
,设平面MBQ的法向量为 ![]() ,由
,由 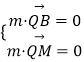 ,得
,得 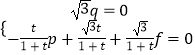 ,取f=t,得
,取f=t,得 ![]() .∴平面MBQ的一个法向量为
.∴平面MBQ的一个法向量为 ![]()
∵二面角M-BQ-C的平面角的大小为30°,∴ 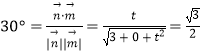 ,解得t=3.
,解得t=3.
【解析】本题主要考查空间直线与平面垂直、平面与平面垂直、直线与直线垂直的判定与性质,二面角等基础知识,考查空间想象能力,推理论证能力,运算求解能力,以及数形结合思想、化归与转化思想.
【考点精析】通过灵活运用直线与平面垂直的判定和平面与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
相关题目