题目内容
下列给出的函数中,既不是奇函数也不是偶函数的是
A.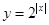 |
B.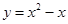 |
C.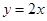 |
D.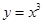 |
B
本题利用直接法解决,即根据判断函数奇偶性的一般步骤:如果定义域不关于原点对称,那么f(x)是非奇非偶函数,当定义域关于原点对称时,求出 f(-x)与-f(x)判断f(-x)=f(x),f(-x)=-f(x)是否成立,如果满足 f(-x)=-f(x),那么 f(x)就是奇函数.如果满足 f(-x)=f(x),那么 f(x)就是偶函数.如果都不满足,那么f(x)是非奇非偶函数.一一进行判定即可.
解:由题意知:A,B,C,D定义域都关于原点对称
A中满足∵y=2|x|
∴f(-x)=2|x|
∴f(-x)=f(x)
∴f(x)是偶函数.
B∵y=x2-x
∴f(-x)=(-x)2-(-x)=x2+x
-f(x)=-(x2-x)
∴f(x)≠f(-x),f(-x)≠-f(x)
故不是奇函数也不是偶函数
C∵y=2x
∴f(-x)=-2x,-f(x)=-2x
∴f(-x)=-f(x)
∴f(x)是奇函数
D∵y=x3
∴f(-x)=(-x)3,-f(x)=-x3
∴f(-x)=-f(x),
∴f(x)是奇函数
故选B

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
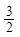 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )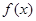 定义域为R,则
定义域为R,则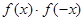 一定为 (
一定为 ( 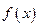 是定义在R上的奇函数,若
是定义在R上的奇函数,若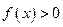 。则以下不等式不一定成立的是 ( )
。则以下不等式不一定成立的是 ( )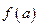 >
>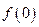
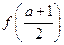 >
>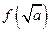
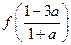 >
>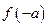
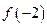
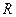 的函数
的函数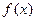 为偶函数,且当
为偶函数,且当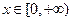 时,
时,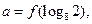
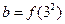 ,
,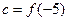 ,则
,则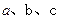 的大小关系是( )
的大小关系是( )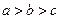
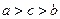
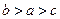
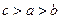
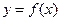 是定义在R上的奇函数,当
是定义在R上的奇函数,当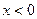 时,
时,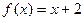 ,那么不等式
,那么不等式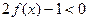 的解集是( )
的解集是( )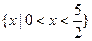
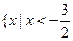 或
或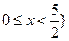
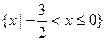
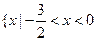 或
或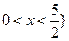
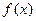 是定义在R上的奇函数,并且当
是定义在R上的奇函数,并且当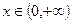 时,
时,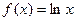 ,那么,
,那么, .
.