题目内容
已知0<k<4,直线l1:kx-2y-2k+8=0和直线l:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则使得这个四边形面积最小的k值为______.
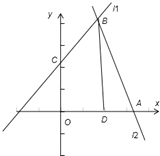
如图所示:
直线l1:kx-2y-2k+8=0 即k(x-2)-2y+8=0,过定点B(2,4),
与y轴的交点C(0,4-k),
直线l:2x+k2y-4k2-4=0,即 2x-4+k2 (y-4)=0,
过定点(2,4 ),与x轴的交点A(2 k2+2,0),
由题意知,四边形的面积等于三角形ABD的面积和梯形 OCBD的面积之和,
故所求四边形的面积为
×4×(2 k2+2-2)+
=4k2-k+8,
∴k=
时,所求四边形的面积最小,
故答案为
.
直线l1:kx-2y-2k+8=0 即k(x-2)-2y+8=0,过定点B(2,4),
与y轴的交点C(0,4-k),
直线l:2x+k2y-4k2-4=0,即 2x-4+k2 (y-4)=0,
过定点(2,4 ),与x轴的交点A(2 k2+2,0),
由题意知,四边形的面积等于三角形ABD的面积和梯形 OCBD的面积之和,
故所求四边形的面积为
| 1 |
| 2 |
| 2×(4-k+4) |
| 2 |
∴k=
| 1 |
| 8 |
故答案为
| 1 |
| 8 |


练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
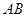 为圆
为圆 的直径,
的直径,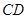 为垂直
为垂直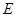 ,弦
,弦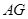 交
交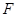 .
.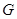 、
、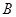 四点共圆;
四点共圆;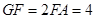 ,求线段
,求线段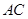 的长.
的长. 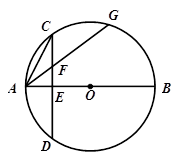

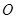 的直径,
的直径,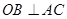 ,弦BN交AC于点M,若
,弦BN交AC于点M,若 ,OM=1,则MN的长为 .
,OM=1,则MN的长为 .