题目内容
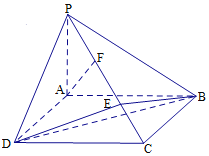
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,![]() ,BD=2.
,BD=2.
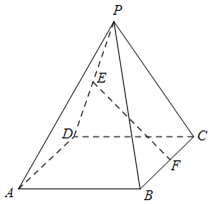
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)取AP的中点为H,连接EH,HB,证明四边形BFEH为平行四边形得到答案.
(2)过A作AN⊥PB于点N,连接NC,AC,BD,设AC交BD于点O,确定则∠ANC 为二面角A﹣PB﹣C 的平面角,计算得到答案.
(1)取AP的中点为H,连接EH,HB;
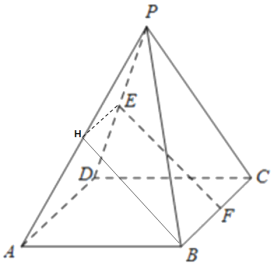
由E,H分别为PD,PA的中点,则EH∥AD且![]() ;
;
又F为BC的中点,则BF∥AD且![]() ;
;
所以EH∥BF且EH=BF,则四边形BFEH为平行四边形;
所以EF∥BH,又HB![]() 平面PAB;
平面PAB;
所以EF∥平面PAB;
(2)过A作AN⊥PB于点N,连接NC,AC,BD,设AC交BD于点O,
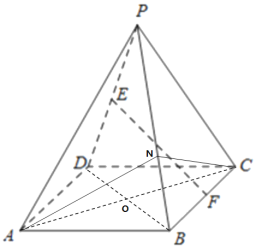
在△PBD中O为AC的中点,PD=PB,则PO⊥BD;
又平面PBD⊥平面ABCD,所以PO⊥平面ABCD;
在△PBD中,PD⊥PB,BD=2.则PD=PB![]() ;
;
由题意有PA=PC![]() ,AO=2,
,AO=2,![]() ,
,
在等腰三角形APB中,![]() ;
;
由△PAB≌△PCB,则CN⊥PB;CN=AN
在△ACN中,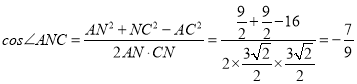 ;
;
故平面PAB与平面PBC所成的锐二面角的余弦值为![]() .
.

【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |
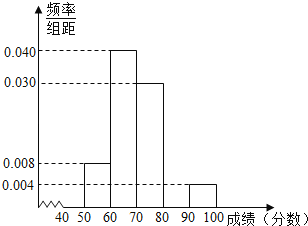
(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.