题目内容
已知函数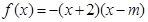 (其中
(其中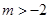 ).
).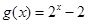 .
.
(1)若命题“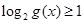 ”是假命题,求
”是假命题,求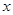 的取值范围;
的取值范围;
(2)设命题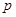 :
: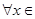
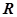 ,
,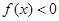 或
或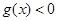 ;命题
;命题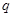 :
: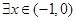 ,
,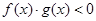 .若
.若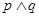 是真命题,求
是真命题,求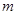 的取值范围.
的取值范围.
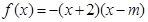 (其中
(其中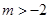 ).
).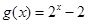 .
.(1)若命题“
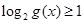 ”是假命题,求
”是假命题,求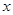 的取值范围;
的取值范围;(2)设命题
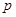 :
: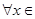
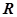 ,
,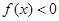 或
或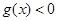 ;命题
;命题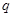 :
: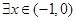 ,
,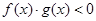 .若
.若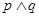 是真命题,求
是真命题,求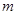 的取值范围.
的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)通过问题的等价转化,然后解一个简单的指、对数不等式即得答案,但是有一个易错之处:“
 ”这里错在不是等价转化,切记去掉对数符号后一定要保证真数为正;(2)解决此问题,对逻辑分析问题的能力要求比较高,首先要掌握逻辑用语的知识,然后还需借助集合的语言来描述,最终回到不等式求解,且需关注细节:端点是否带等号,这样才能善始善终.
”这里错在不是等价转化,切记去掉对数符号后一定要保证真数为正;(2)解决此问题,对逻辑分析问题的能力要求比较高,首先要掌握逻辑用语的知识,然后还需借助集合的语言来描述,最终回到不等式求解,且需关注细节:端点是否带等号,这样才能善始善终.试题解析:(1)命题“
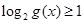 ”是假命题,则
”是假命题,则 , 2分
, 2分即
 ,
, ,解得
,解得 5分
5分(2)因为
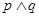 是真命题,则
是真命题,则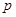 和
和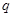 都为真命题. 6分
都为真命题. 6分法一:因为
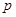 是真命题,则
是真命题,则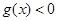 的解集的补集是
的解集的补集是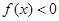 解集的子集;
解集的子集;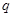 是真命题,则
是真命题,则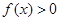 的解集与
的解集与 的交集非空.
的交集非空.①若
 ,则
,则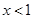 .
.又∵
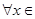
 ,
, 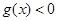 或
或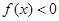 ,
,∴
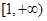 是
是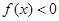 的解集的子集.
的解集的子集.又由
 (其中
(其中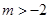 ),解得得
),解得得 或
或 ,
,因此
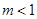 . 9分
. 9分②∵当
 时,
时, ,
,∴问题转化为
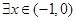 ,使得
,使得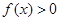 ,
,即
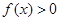 的解集与
的解集与 的交集非空.
的交集非空.即
 ,则
,则 , 13分
, 13分综合①②可知满足条件的
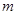 的取值范围是
的取值范围是 14分
14分法二:当
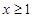 时,
时,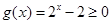 ,因为
,因为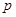 是真命题,则
是真命题,则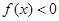 ,
,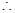
 ,即
,即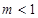 9分
9分当
 时,
时, ,因为
,因为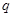 是真命题,则
是真命题,则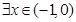 ,使
,使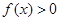 ,
,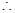
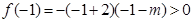 ,即
,即 13分
13分综上所述,
 . 14分
. 14分
练习册系列答案
相关题目
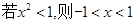 ”的逆否命题是( )
”的逆否命题是( )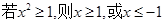
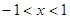 ,则
,则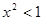
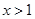 或
或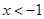 ,则
,则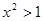
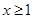 或
或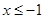 ,则
,则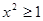
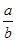 =-1
=-1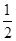 ,
,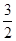 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.