题目内容
设过抛物线 的焦点F的弦PQ,则以PQ为直径的圆与抛物线准线的位置关系是( )
的焦点F的弦PQ,则以PQ为直径的圆与抛物线准线的位置关系是( )
 的焦点F的弦PQ,则以PQ为直径的圆与抛物线准线的位置关系是( )
的焦点F的弦PQ,则以PQ为直径的圆与抛物线准线的位置关系是( )| A.相交 | B.相切 |
| C.相离 | D.以上答案均有可能 |
B
解:设PQ的中点是M,M到准线的距离是d.
而P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.
又M到准线的距离d是梯形的中位线,故有d="(|PF|+|QF|" )/2 ="|PQ|" /2 .
即圆心M到准线的距离等于半径|PQ|/ 2 ,
所以圆与准线是相切.
故选B.
而P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.
又M到准线的距离d是梯形的中位线,故有d="(|PF|+|QF|" )/2 ="|PQ|" /2 .
即圆心M到准线的距离等于半径|PQ|/ 2 ,
所以圆与准线是相切.
故选B.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
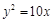 的焦点到准线的距离是( ).
的焦点到准线的距离是( ).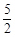
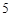
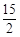
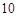
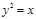 上的点到直线
上的点到直线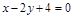 的距离最小的点的坐标是 .
的距离最小的点的坐标是 . 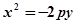 的焦点坐标为
的焦点坐标为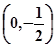 ,它与过点
,它与过点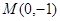 的直线
的直线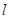 相交于A,B两点,O为坐标原点。
相交于A,B两点,O为坐标原点。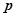 值;
值;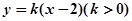 与抛物线
与抛物线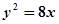 相交于
相交于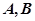 两点,
两点,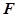 为抛物线的焦点,若
为抛物线的焦点,若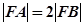 ,则
,则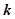 的值为 ______________.
的值为 ______________.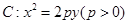 的焦点为
的焦点为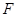 ,准线为
,准线为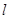 ,
,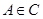 ,已知以
,已知以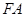 为半径的圆
为半径的圆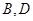 两点;
两点;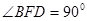 ,
,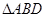 的面积为
的面积为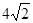 ;求
;求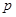 的值及圆
的值及圆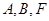 三点在同一直线
三点在同一直线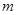 上,直线
上,直线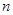 与
与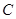 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到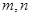 距离的比值.
距离的比值.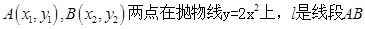 的垂直平分线.
的垂直平分线.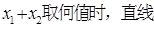
 ?
? 轴上截距的取值范围.
轴上截距的取值范围.  的焦点
的焦点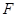 的直线
的直线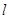 交
交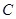 于
于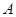 、
、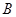 两点(点
两点(点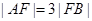 ,则
,则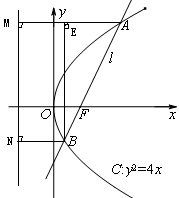
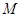 到点
到点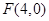 的距离比它到定直线
的距离比它到定直线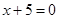 的距离小1,则点
的距离小1,则点