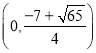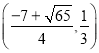Question

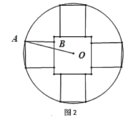
【题目】从秦朝统一全国币制到清朝末年，圆形方孔铜钱（简称“孔方兄”）是我国使用时间长达两千多年的货币．如图1，这是一枚清朝同治年间的铜钱，其边框是由大小不等的两同心圆围成的，内嵌正方形孔的中心与同心圆圆心重合，正方形外部，圆框内部刻有四个字“同治重宝”．某模具厂计划仿制这样的铜钱作为纪念品，其小圆内部图纸设计如图2所示，小圆直径1厘米，内嵌一个大正方形孔，四周是四个全等的小正方形（边长比孔的边长小），每个正方形有两个顶点在圆周上，另两个顶点在孔边上，四个小正方形内用于刻铜钱上的字．设，五个正方形的面积和为S．

（1）求面积S关于的函数表达式，并求定义域；

（2）求面积S的最小值及此时的值．

Answer 1

【答案】（1），的取值范围为，，；（2）时，面积S有最小值为．

【解析】

（1）构造直角三角形，利用小圆直径与三角函数分别求出大、小正方形的边长，即可求得五个正方形的面积表达式，由小正方形边长小于内嵌一个大正方形的边长可求得的取值范围；（2）利用降幂公式及辅助角公式化简面积表达式为正弦型函数，当时S取最小值，此时求出的值然后求出，由二倍角的正弦公式可求得.

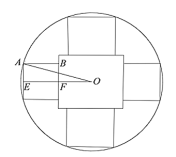
（1）过点O分别作小正方形边，大正方形边的垂线，垂足分别为E，F，

因为内嵌一个大正方形孔的中心与同心圆圆心重合，

所以点E，F分别为小正方形和大正方形边的中点，

所以小正方形的边长为，

大正方形的边长为，

所以五个正方形的面积和为，

，

因为小正方形边长小于内嵌一个大正方形的边长，

所以，，，

所以的取值范围为，，

所以面积S关于的函数表达式为，

的取值范围为，，．

（2）法一：，

，

，

，其中，，

所以，此时，因为，所以

，所以，

所以，

则，化简得：，

由此解得：，

因为，所以，

答：面积S最小值为，

法二：，

，

令，则，

设，，

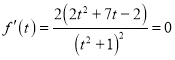令，得：，

t
	-	0	+
		极小值

所以时，面积S最小值为.