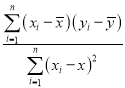题目内容
【题目】在![]() 中,
中,![]() 且
且![]() ,
,![]() 边上的中线长为
边上的中线长为![]() ,则
,则![]() 的面积是________.
的面积是________.
【答案】![]()
【解析】
根据题意,将![]() 变形可得
变形可得![]() ,又由
,又由![]() ,则
,则![]() 可以变形为
可以变形为![]() ,分析可得
,分析可得![]() 的值,进而可得
的值,进而可得![]() 的值,分析可得,
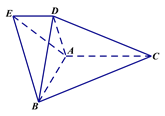
的值,分析可得,![]() 为等腰三角形,设
为等腰三角形,设![]() 为
为![]() 中点,AD=
中点,AD=![]() ,设
,设![]() ,在△ACD中,由余弦定理可得cosC=
,在△ACD中,由余弦定理可得cosC=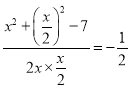 ,计算可得
,计算可得![]() 的值,由三角形面积公式计算可得答案.
的值,由三角形面积公式计算可得答案.
根据题意,![]() 中,
中,![]() ,则有
,则有![]() sinB=
sinB=![]() ,变形可得sinB=1+cosC,
,变形可得sinB=1+cosC,
则有cosC=sinB﹣1<0,则C为钝角,B为锐角.
又由A=![]() ,得B+C=
,得B+C=![]() ,则sinB=1+cosCsin(
,则sinB=1+cosCsin(![]() ﹣C)=1+cosCcos(C+
﹣C)=1+cosCcos(C+![]() )=﹣1,
)=﹣1,
又C为钝角,所以C=![]() ,B=
,B=![]() ﹣C=
﹣C=![]() ,
,
则在![]() 中,A=B=
中,A=B=![]() ,则有AC=BC,即
,则有AC=BC,即![]() 为等腰三角形,
为等腰三角形,
设D为BC中点,则AD=![]() ,设AC=x,则有cosC=
,设AC=x,则有cosC=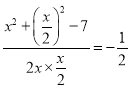 ,解得x=2,即AC=BC=2.
,解得x=2,即AC=BC=2.
则S△ABC=![]() ×AC×BC×sinC=
×AC×BC×sinC=![]() ×2×2×sin
×2×2×sin![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目