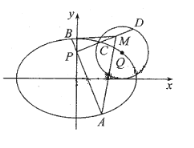
题目内容
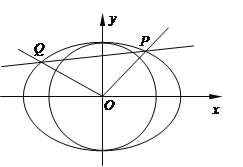
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为
的半径为![]() ,点
,点![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)确定圆![]() 的方程,就是确定半径的值,因为直线
的方程,就是确定半径的值,因为直线![]() 与圆
与圆![]() 相切,所以先确定直线方程,即确定点
相切,所以先确定直线方程,即确定点![]() 坐标:因为
坐标:因为![]() 轴,所以
轴,所以![]() ,根据对称性,可取
,根据对称性,可取![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,根据圆心到切线距离等于半径得
,根据圆心到切线距离等于半径得![]() (2)根据垂径定理,求直线
(2)根据垂径定理,求直线![]() 被圆
被圆![]() 截得弦长的最大值,就是求圆心
截得弦长的最大值,就是求圆心![]() 到直线
到直线![]() 的距离的最小值. 设直线
的距离的最小值. 设直线![]() 的方程为
的方程为![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,利用
,利用![]() 得
得![]() ,化简得
,化简得![]() ,利用直线方程与椭圆方程联立方程组并结合韦达定理得
,利用直线方程与椭圆方程联立方程组并结合韦达定理得![]() ,因此
,因此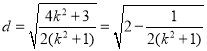 ,当
,当![]() 时,
时,![]() 取最小值,
取最小值,![]() 取最大值为
取最大值为![]() .
.
试题解析:解:(1)
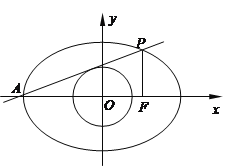
因为椭圆![]() 的方程为
的方程为![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() 轴,所以
轴,所以![]() ,而直线
,而直线![]() 与圆
与圆![]() 相切,
相切,
根据对称性,可取![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
由圆![]() 与直线
与直线![]() 相切,得
相切,得![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)
易知,圆![]() 的方程为
的方程为![]() .
.
①当![]() 轴时,
轴时,![]() ,
,
所以![]() ,
,
此时得直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
②当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
首先由![]() ,得
,得![]() ,
,
即![]() ,
,
所以![]() (*).
(*).
联立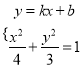 ,消去
,消去![]() ,得
,得![]() ,
,
将![]() 代入(*)式,
代入(*)式,
得![]() .
.
由于圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,故当
,故当![]() 时,
时,![]() 有最大值为
有最大值为![]() .
.
综上,因为![]() ,所以直线
,所以直线![]() 被圆
被圆![]() 截得的弦长的最大值为
截得的弦长的最大值为![]() .
.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目