题目内容
【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]()
![]() ,将
,将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置. 在翻折过程中,下列结论成立的是( )
的位置. 在翻折过程中,下列结论成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
【答案】D
【解析】
利用反证法可证明A、B错误,当![]() 且二面角
且二面角![]() 为直二面角时,计算可得
为直二面角时,计算可得![]() ,从而C错误,利用体积的计算公式及放缩法可得
,从而C错误,利用体积的计算公式及放缩法可得![]() ,从而可求
,从而可求![]() 的最大值为
的最大值为![]() ,因此D正确.
,因此D正确.
对于A,假设存在![]() ,使得
,使得![]() 平面
平面![]() ,
,
如图1所示,
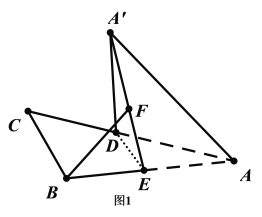
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,故
,故![]() ,
,
但在平面![]() 内,
内,![]() 是相交的,
是相交的,
故假设错误,即不存在![]() ,使得
,使得![]() 平面
平面![]() ,故A错误.
,故A错误.
对于B,如图2,
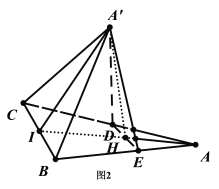
取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,
,
因为![]() 为等边三角形,故
为等边三角形,故![]() ,
,
因为![]() ,故
,故![]()
所以![]() 均为等边三角形,故
均为等边三角形,故![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,故
,故![]() 共线,
共线,
所以![]() ,因为
,因为![]() ,故
,故![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
若某个位置,满足平面![]() 平面
平面![]() ,则
,则![]() 在平面
在平面![]() 的射影在
的射影在![]() 上,也在
上,也在![]() 上,故
上,故![]() 在平面
在平面![]() 的射影为
的射影为![]() ,所以
,所以![]() ,
,
此时![]() ,这与
,这与![]() 矛盾,故B错误.
矛盾,故B错误.
对于C,如图3(仍取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() )
)
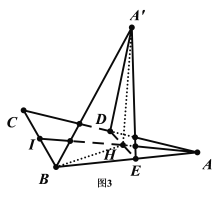
因为![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
因为二面角![]() 为直二面角,故
为直二面角,故![]() ,所以
,所以![]() ,
,
而![]() ,故
,故![]() 平面
平面![]() ,因
,因![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,故C错.
,故C错.
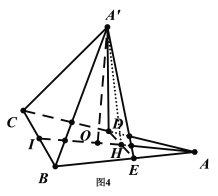
对于D,如图4(仍取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ),
),
作![]() 在底面
在底面![]() 上的射影
上的射影![]() ,则
,则![]() 在
在![]() 上.
上.
因为![]() ,所以
,所以![]() 且
且![]() ,所以
,所以![]() 其
其![]() .
.
又![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
当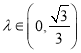 时,
时,![]() ;当
;当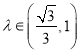 时,
时,![]() .
.
所以![]() 在
在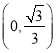 为增函数,在
为增函数,在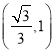 为减函数,故
为减函数,故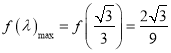 .
.
故D正确.
故选:D.

练习册系列答案
相关题目