题目内容
【题目】已知![]() ,给定
,给定![]() 个整点
个整点![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,从上面的
时,从上面的![]() 个整点中任取两个不同的整点
个整点中任取两个不同的整点![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)从上面![]() 个整点中任取
个整点中任取![]() 个不同的整点,
个不同的整点,![]() .
.
(i)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() ;
;
(ii)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)详见解析;(ii)详见解析.
;(Ⅱ)(i)详见解析;(ii)详见解析.
【解析】
(Ⅰ)列出所有的整点后可得![]() 的所有可能值.
的所有可能值.
(Ⅱ)对于(i),可用反证法,对于(ii),可设直线![]() 上选择了
上选择了![]() 个的点,计算可得诸直线上不同两点的横坐标和的不同个数的最小值为
个的点,计算可得诸直线上不同两点的横坐标和的不同个数的最小值为![]() ,结合
,结合![]() 中任意不同两项之和的不同的值恰有
中任意不同两项之和的不同的值恰有![]() 个可得至少有一个和出现两次,从而可证结论成立.
个可得至少有一个和出现两次,从而可证结论成立.
解:(Ⅰ)当![]() 时,4个整点分别为
时,4个整点分别为![]() .
.
所以![]() 的所有可能值
的所有可能值![]() .
.
(Ⅱ)(i)假设不存在互不相同的四个整点![]() ,
,
满足![]() .
.
即在直线![]() 中至多有一条直线上取多于1个整点,其余每条直线上至多取一个整点, 此时符合条件的整点个数最多为
中至多有一条直线上取多于1个整点,其余每条直线上至多取一个整点, 此时符合条件的整点个数最多为![]() .
.
而![]() ,与已知
,与已知![]() 矛盾.
矛盾.
故存在互不相同的四个整点![]() ,满足
,满足![]() .
.
(ii)设直线![]() 上有
上有![]() 个选定的点.
个选定的点.
若![]() ,设
,设![]() 上的这
上的这![]() 个选定的点的横坐标为
个选定的点的横坐标为![]() ,且满足
,且满足![]() .
.
由![]() ,
,
知![]() 中任意不同两项之和至少有
中任意不同两项之和至少有![]() 个不同的值,这对于
个不同的值,这对于![]() 也成立.
也成立.
由于![]() 中任意不同两项之和的不同的值恰有
中任意不同两项之和的不同的值恰有![]() 个,
个,
而![]() ,
,
可知存在四个不同的点![]() ,
,
满足![]() .
.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,居民用水原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用水范围(吨) |
|
|
|
为了了解全市居民月用水量的分布情况,通过抽样,获得了![]() 户居民的月用水量(单位:吨),得到统计表如下:
户居民的月用水量(单位:吨),得到统计表如下:
居民用水户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用水量(吨) | 7 | 8 | 8 | 9 | 10 | 11 | <>13 | 14 | 15 | 20 |
(1)若用水量不超过![]() 吨时,按
吨时,按![]() 元/吨计算水费;若用水量超过
元/吨计算水费;若用水量超过![]() 吨且不超过
吨且不超过![]() 吨时,超过
吨时,超过![]() 吨部分按
吨部分按![]() 元/吨计算水费;若用水量超过
元/吨计算水费;若用水量超过![]() 吨时,超过
吨时,超过![]() 吨部分按
吨部分按![]() 元/吨计算水费.试计算:若某居民用水
元/吨计算水费.试计算:若某居民用水![]() 吨,则应交水费多少元?
吨,则应交水费多少元?
(2)现要在这![]() 户家庭中任意选取
户家庭中任意选取![]() 户,求取到第二阶梯水量的户数的分布列与期望;
户,求取到第二阶梯水量的户数的分布列与期望;
(3)用抽到的![]() 户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取
户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取![]() 户,若抽到
户,若抽到![]() 户月用水量为第一阶梯的可能性最大,求
户月用水量为第一阶梯的可能性最大,求![]() 的值.
的值.
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
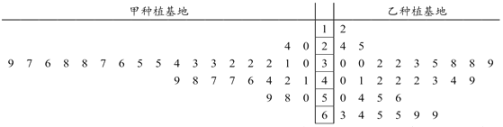
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?