题目内容
已知函数f(x)=ln(x+1)-x2-x.
(1)若关于x的方程f(x)=-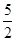 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(2)证明:对任意的正整数n,不等式2+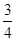 +
+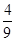 +…+
+…+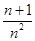 >ln(n+1)都成立.
>ln(n+1)都成立.
(1)若关于x的方程f(x)=-
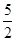 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;(2)证明:对任意的正整数n,不等式2+
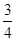 +
+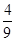 +…+
+…+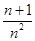 >ln(n+1)都成立.
>ln(n+1)都成立.(1) ln 3-1≤b<ln 2+ . (2)见解析
. (2)见解析
 . (2)见解析
. (2)见解析(1)f(x)=ln(x+1)-x2-x,由f(x)=-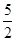 x+b,得ln(x+1)-x2+
x+b,得ln(x+1)-x2+ x-b=0,
x-b=0,
令φ(x)=ln(x+1)-x2+ x-b,则f(x)=-
x-b,则f(x)=-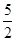 x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)=
x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)= -2x+
-2x+ =
=  ,
,
当x∈[0,1)时,φ′(x)>0,于是φ(x)在[0,1)上单调递增;
当x∈(1,2]时,φ′(x)<0,于是φ(x)在(1,2]上单调递减.
依题意有
解得ln 3-1≤b<ln 2+ .
.
(2)证明:方法一,f(x)=ln(x+1)-x2-x的定义域为{x|x>-1},则有f′(x)= ,
,
令f′(x)=0,得x=0或x=- (舍去),
(舍去),
当-1<x<0时,f′(x)>0,f(x)单调递增;
当x>0时,f′(x)<0,f(x)单调递减.
∴f(0)为f(x)在(-1,+∞)上的最大值.
∴f(x)≤f(0),故ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立).
对任意正整数n,取x= >0得,ln
>0得,ln <
< +
+ ,
,
∴ln <
<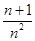 .
.
故2+ +…+
+…+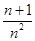 ≥ln 2+ln
≥ln 2+ln +…+ln
+…+ln  =ln(n+1).
=ln(n+1).
方法二,数学归纳法证明:
当n=1时,左边= =2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.
=2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.
假设当n=k(k∈N*,k≥1)时,2+ >ln(k+1)成立,
>ln(k+1)成立,
则当n=k+1时,有2+ +ln(k+1).
+ln(k+1).
做差比较:ln(k+2)-ln(k+1)- =ln
=ln  -
- =ln
=ln -
- .
.
构建函数F(x)=ln(1+x)-x-x2,x∈(0,1),
则F′(x)= <0,
<0,
∴F(x)在(0,1)上单调递减,∴F(x)<F(0)=0.
取x= (k≥1,k∈N*),ln
(k≥1,k∈N*),ln -
- <F(0)=0.
<F(0)=0.
即ln(k+2)-ln(k+1)- <0,
<0,
亦即 +ln(k+1)>ln(k+2),
+ln(k+1)>ln(k+2),
故n=k+1时,有2+ +ln(k+1)>ln(k+2),不等式也成立.
+ln(k+1)>ln(k+2),不等式也成立.
综上可知,对任意的正整数,不等式都成立.
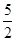 x+b,得ln(x+1)-x2+
x+b,得ln(x+1)-x2+ x-b=0,
x-b=0,令φ(x)=ln(x+1)-x2+
 x-b,则f(x)=-
x-b,则f(x)=-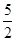 x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)=
x+b在区间[0,2]上恰有两个不同的实数根等价于φ(x)=0在区间[0,2]上恰有两个不同的实数根,φ′(x)= -2x+
-2x+ =
=  ,
, 当x∈[0,1)时,φ′(x)>0,于是φ(x)在[0,1)上单调递增;
当x∈(1,2]时,φ′(x)<0,于是φ(x)在(1,2]上单调递减.
依题意有

解得ln 3-1≤b<ln 2+
 .
.(2)证明:方法一,f(x)=ln(x+1)-x2-x的定义域为{x|x>-1},则有f′(x)=
 ,
,令f′(x)=0,得x=0或x=-
 (舍去),
(舍去),当-1<x<0时,f′(x)>0,f(x)单调递增;
当x>0时,f′(x)<0,f(x)单调递减.
∴f(0)为f(x)在(-1,+∞)上的最大值.
∴f(x)≤f(0),故ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立).
对任意正整数n,取x=
 >0得,ln
>0得,ln <
< +
+ ,
,∴ln
 <
<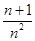 .
.故2+
 +…+
+…+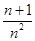 ≥ln 2+ln
≥ln 2+ln +…+ln
+…+ln  =ln(n+1).
=ln(n+1).方法二,数学归纳法证明:
当n=1时,左边=
 =2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.
=2,右边=ln(1+1)=ln 2,显然2>ln 2,不等式成立.假设当n=k(k∈N*,k≥1)时,2+
 >ln(k+1)成立,
>ln(k+1)成立,则当n=k+1时,有2+
 +ln(k+1).
+ln(k+1).做差比较:ln(k+2)-ln(k+1)-
 =ln
=ln  -
- =ln
=ln -
- .
.构建函数F(x)=ln(1+x)-x-x2,x∈(0,1),
则F′(x)=
 <0,
<0,∴F(x)在(0,1)上单调递减,∴F(x)<F(0)=0.
取x=
 (k≥1,k∈N*),ln
(k≥1,k∈N*),ln -
- <F(0)=0.
<F(0)=0.即ln(k+2)-ln(k+1)-
 <0,
<0,亦即
 +ln(k+1)>ln(k+2),
+ln(k+1)>ln(k+2),故n=k+1时,有2+
 +ln(k+1)>ln(k+2),不等式也成立.
+ln(k+1)>ln(k+2),不等式也成立.综上可知,对任意的正整数,不等式都成立.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
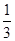 x3-
x3-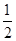 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.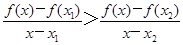 .
.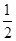 x2-
x2- 的取值范围.
的取值范围.
 是函数
是函数 (
( )的两个极值点
)的两个极值点 ,求函数
,求函数 的解析式;
的解析式; ,求
,求 的最大值。
的最大值。 .
. ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围; .
.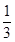 x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______. 、
、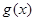 都是定义在R上的函数,
都是定义在R上的函数, ,
,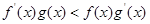 ,
,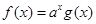 ,
, ,则关于x的方程
,则关于x的方程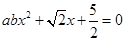 (
(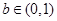 )有两个不同实根的概率为 .
)有两个不同实根的概率为 .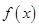 的定义域为
的定义域为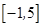 ,部分对应值如下表,
,部分对应值如下表, 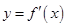 的图象如图所示. 下列关于
的图象如图所示. 下列关于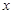
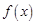
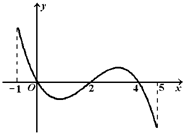
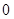 ,
,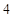 ;
;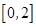 上是减函数;
上是减函数;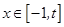 时,
时,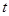 的最大值为4;
的最大值为4;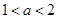 时,函数
时,函数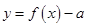 有
有