题目内容
3．某几何体的三视图如图所示，则该几何体的体积是（ ）
| A． | 2 | B． | $\frac{8}{3}$ | C． | 4 | D． | $\frac{20}{9}$ |
分析 由三视图知：几何体是四棱锥，如图所示，求出相应数据即可求出几何体的体积．
解答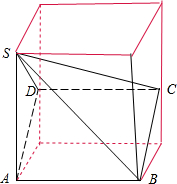 
解：由三视图知：几何体是四棱锥，如图所示，
ABCD的面积为2×$\sqrt{5}$=2$\sqrt{5}$，
△SAD中，SD=AD=$\sqrt{5}$，SA=2，
∴cos∠SDA=$\frac{5+5-4}{2\sqrt{5}×\sqrt{5}}$=$\frac{3}{5}$，
∴sin∠SDA=$\frac{4}{5}$，
∴S△SAD=$\frac{1}{2}×\sqrt{5}×\sqrt{5}×\frac{4}{5}$=2
设S到平面ABCD的距离为h，则$\frac{1}{2}×\sqrt{5}h$=2，
∴h=$\frac{4}{\sqrt{5}}$
所以几何体的体积是$\frac{1}{3}×2\sqrt{5}×\frac{4}{\sqrt{5}}$=$\frac{8}{3}$，
故选：B．
点评 本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
相关题目