题目内容
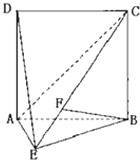
【题目】如图，直二面角
中，四边形ABCD是边长为2的正方形，
，F为CE上的点，且
平面ACE．
Ⅰ
求证：
平面BCE；
Ⅱ求二面角
的余弦值；
Ⅲ求点D到平面ACE的距离．
【答案】（I）详见解析；（II）
；（III）
.
【解析】
要证明
平面BCE，需要在平面BCE内找两条相交直线都垂直于
，而易证
；
求二面角
的余弦值，需要先作角，连接BD交AC交于G，连接FG，可证得
是二面的平面角，在
中求解即可；
求点D到平面ACE的距离，可以转化为求三棱锥
的高用等体积法求出即可。
解：
平面
二面角
为直二面角
且
．
平面
平面
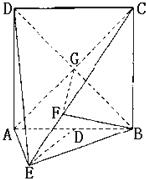
连接BD交AC交于G，连接FG
正方形ABCD边长为
，
平面
由三垂线定理的逆定理得
．
是二面的平面角
平面BCE，
又
，
在等腰直角三角形AEB中，
又
中，
中
二面角的正弦值等于
过点E作
交AB于点O，
二面角为直二面角，
平面ABCD
设D到平面ACE的距离为h，由
，可得
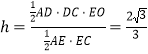
点D到平面ACE的距离为
练习册系列答案
相关题目
