题目内容
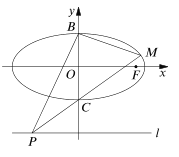
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.

(1)求实数![]() 的值;
的值;
(2)求以点![]() 为圆心,且与抛物线
为圆心,且与抛物线![]() 的准线相切的圆的方程.
的准线相切的圆的方程.
【答案】(1)b=-1.(2)(x-2)2+(y-1)2=4.
【解析】
试题分析:(1)整理直线![]() 和抛物线
和抛物线![]() 的方程构成的方程组,利用
的方程构成的方程组,利用![]() 即可求得
即可求得![]() 的值;(2)由(1)的结论即可求得圆心
的值;(2)由(1)的结论即可求得圆心![]() ,根据圆与抛物线的准线相切得到圆的半径,即可写出圆的标准方程.
,根据圆与抛物线的准线相切得到圆的半径,即可写出圆的标准方程.
试题解析:(1))由![]() 得x2-4x-4b=0.(*)
得x2-4x-4b=0.(*)
因为直线l与抛物线C相切,所以Δ=(-4)2-4×(-4b)=0,解得b=-1.
(2)由(1)可知b=-1,故方程(*)即为x2-4x+4=0,解得x=2.将其代入x2=4y,得y=1.
故点A(2,1).因为圆A与抛物线C的准线相切,
所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离,
即r=|1-(-1)|=2,所以圆A的方程为(x-2)2+(y-1)2=4.

练习册系列答案
相关题目
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |

A.1
B.![]()
C.![]()
D.![]()