题目内容
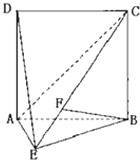
【题目】抛物线C的方程为y=ax2(a<0),过抛物线C上一点P(x0 , y0)(x0≠0)作斜率为k1 , k2的两条直线分别交抛物线C于A(x1 , y1)B(x2 , y2)两点(P,A,B三点互不相同),且满足k2+λk1=0(λ≠0且λ≠﹣1).
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ![]() =λ
=λ ![]() ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当λ=1时,若点P的坐标为(1,﹣1),求∠PAB为钝角时点A的纵坐标y1的取值范围.
【答案】解:(Ⅰ)由抛物线C的方程y=ax2(a<0)得,焦点坐标为(0, ![]() ),准线方程为y=﹣
),准线方程为y=﹣ ![]() .
.
(Ⅱ)证明:设直线PA的方程为y﹣y0=k1(x﹣x0),直线PB的方程为y﹣y0=k2(x﹣x0).
点P(x0 , y0)和点A(x1 , y1)的坐标是方程组  的解.
的解.
将②式代入①式得ax2﹣k1x+k1x0﹣y0=0,于是x1+x0= ![]() ,故x1=
,故x1= ![]() ﹣x0 ③.
﹣x0 ③.
又点P(x0 , y0)和点B(x2 , y2)的坐标是方程组 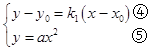 的解.
的解.
将⑤式代入④式得ax2﹣k2x+k2x0﹣y0=0.于是x2+x0= ![]() ,故x2=
,故x2= ![]() ﹣x0 .
﹣x0 .
由已知得,k2=﹣λk1 , 则x2=﹣ ![]() ﹣x0 . ⑥
﹣x0 . ⑥
设点M的坐标为(xM , yM),由 ![]() =λ
=λ ![]() ,可得 xM=
,可得 xM= ![]() .
.
将③式和⑥式代入上式得xM= ![]() =﹣x0 ,
=﹣x0 ,
即xM+x0=0.所以线段PM的中点在y轴上.
(Ⅲ)因为点P(1,﹣1)在抛物线y=ax2上,所以a=﹣1,抛物线方程为y=﹣x2 .
由③式知x1=﹣k1﹣1,代入y=﹣x2 得 y1=﹣(k1+1)2 .
将λ=1代入⑥式得 x2=k1﹣1,代入y=﹣x2得 y2=﹣(k2+1)2 .
因此,直线PA、PB分别与抛物线C的交点A、B的坐标为A(﹣k1﹣1,﹣k12﹣2k1﹣1),B(k1﹣1,﹣k12+2k1﹣1).
于是 ![]() =(k1+2,k12+2k1),
=(k1+2,k12+2k1), ![]() =(2k1 , 4k1),
=(2k1 , 4k1),![]() =2k1(k1+2)+4k1(k12+2k1)=2(k1+2)(2+k11).
=2k1(k1+2)+4k1(k12+2k1)=2(k1+2)(2+k11).
因∠PAB为钝角且P、A、B三点互不相同,故必有 ![]() <0./span>
<0./span>
求得k1的取值范围是k1<﹣2,或﹣ ![]() <k1<0.
<k1<0.
又点A的纵坐标y1满足y1=﹣(k1+1)2 , 故当k1<﹣2时,y1<﹣1;当﹣ ![]() <k1<0时,﹣1<y<﹣
<k1<0时,﹣1<y<﹣ ![]() .
.
即y1∈(﹣∞,﹣1)∪(﹣1,﹣ ![]() ).
).
【解析】(Ⅰ)数形结合,依据抛物线C的标准方程写焦点坐标和准线方程.(Ⅱ)先依据条件求出点M的横坐标,利用一元二次方程根与系数的关系,证明xM+x0=0.(Ⅲ)∠PAB为钝角时,必有 ![]() <0.用k1表示y1 , 通过k1的范围来求y1的范围.
<0.用k1表示y1 , 通过k1的范围来求y1的范围.

 口算能手系列答案
口算能手系列答案【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于 60分 | 60分 到79分 | 80分 到89分 | 不低 于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
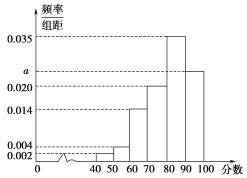
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)在等级为不满意市民中,老年人占![]() ,中青年占
,中青年占![]() ,现从该等级市民中按年龄分层抽取
,现从该等级市民中按年龄分层抽取![]() 人了解不满意的原因,并从中选取
人了解不满意的原因,并从中选取![]() 人担任整改督导员,求至少有一位老年督导员的概率;
人担任整改督导员,求至少有一位老年督导员的概率;
(3)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.![]()
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |

A.1
B.![]()
C.![]()
D.![]()