题目内容
2.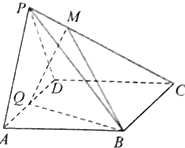 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.( I)求证:QB⊥PD;
(Ⅱ)点M在线段PC上,且QM⊥PC,求M-QB-C的余弦值.
分析 (I)连接PQ,BD,利用菱形与等边三角形的性质可得;BQ⊥AD.在△PAD中,PA=PD=$\sqrt{2}$,Q为AD的中点,AD=2,可得PQ=1.
由PQ2+BQ2=PB2,可得BQ⊥PQ.利用线面垂直的判定定理可得BQ⊥平面PAD,即可证明.
(II)如图,以点Q为坐标原点,分别以QA,QB,QP为x,y,z轴建立空间直角坐标系.A(1,0,0),B$(0,\sqrt{3},0)$,$C(-2,\sqrt{3},0)$,Q(0,0,0),P(0,0,1),点M在PC上,设$\overrightarrow{PM}=t\overrightarrow{PC}$,$\overrightarrow{PC}$=$(-2,\sqrt{3},-1)$.$\overrightarrow{QM}$=$\overrightarrow{QP}+\overrightarrow{PM}$=$(-2t,\sqrt{3}t,1-t)$,利用$\overrightarrow{QM}⊥\overrightarrow{PC}$,可得$\overrightarrow{QM}•\overrightarrow{PC}$=0,解得t.平面MQB的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{QB}=0}\\{\overrightarrow{m}•\overrightarrow{QM}=0}\end{array}\right.$,解得$\overrightarrow{m}$,取底面ABCD的法向量$\overrightarrow{n}$=(0,0,1),利用$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$即可得出.
解答 (I)证明:连接PQ,BD,∵△ABD是正三角形,Q为AD的中点,
∴BQ⊥AD.
∴BQ=$\sqrt{3}$.
在△PAD中,PA=PD=$\sqrt{2}$,Q为AD的中点,AD=2,
∴PQ=$\sqrt{P{A}^{2}-A{Q}^{2}}$=1.
∴PQ2+BQ2=PB2,
∴BQ⊥PQ.又PQ∩AD=Q,
∴BQ⊥平面PAD,
∴QB⊥PD.
(II)解:如图,以点Q为坐标原点,分别以QA,QB,QP为x,y,z轴建立空间直角坐标系.
A(1,0,0),B$(0,\sqrt{3},0)$,$C(-2,\sqrt{3},0)$,Q(0,0,0),P(0,0,1),
点M在PC上,设$\overrightarrow{PM}=t\overrightarrow{PC}$,$\overrightarrow{PC}$=$(-2,\sqrt{3},-1)$.
∴$\overrightarrow{PM}$=$(-2t,\sqrt{3}t,-t)$.$\overrightarrow{QM}$=$\overrightarrow{QP}+\overrightarrow{PM}$=$(-2t,\sqrt{3}t,1-t)$,
∵$\overrightarrow{QM}⊥\overrightarrow{PC}$,
∴$\overrightarrow{QM}•\overrightarrow{PC}$=0,
∴4t+3t-(1-t)=0,解得t=$\frac{1}{8}$,
∴$\overrightarrow{QM}=(-\frac{1}{4},\frac{\sqrt{3}}{8},\frac{7}{8})$,$\overrightarrow{QB}$=$(0,\sqrt{3},0)$,
设平面MQB的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{QB}=0}\\{\overrightarrow{m}•\overrightarrow{QM}=0}\end{array}\right.$,化为$\left\{\begin{array}{l}{y=0}\\{-2x+\sqrt{3}y+7z=0}\end{array}\right.$,
令z=2,解得x=7,y=0,∴$\overrightarrow{m}$=(7,0,2),
取底面ABCD的法向量$\overrightarrow{n}$=(0,0,1),
$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2}{1×\sqrt{53}}$=$\frac{2\sqrt{53}}{53}$.
∴二面角M-QB-C的余弦值为$\frac{2\sqrt{53}}{53}$.
点评 本题考查了线面面面垂直的判定与性质定理、菱形与等边三角形的性质、勾股定理的逆定理、向量的线性运算、向量垂直与数量积的关系,考查了通过建立空间直角坐标系利用平面的法向量的夹角得出二面角的方法,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案 如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.
如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.