题目内容
14.如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=$\frac{1}{2}$AP=2,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使得PD⊥平面ABCD.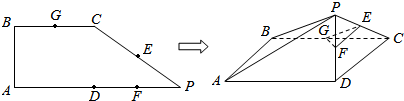
(1)求证:平面PCD⊥平面PAD;
(2)求面GEF与面EFD所成锐二面角的大小.
分析 (1)由PD⊥平面ABCD,可得PD⊥CD,又CD⊥AD,可得CD⊥平面PAD,利用面面垂直的判定定理即可证明;
(2)如图以D为原点,以DA,DC,DP分别为x,y,z轴建立空间直角坐标系D-xyz.不妨设AB=BC=$\frac{1}{2}AP$=2.则G(1,2,0),E(0,1,1),F(0,0,1),
$\overrightarrow{EF}$=(0,-1,0),$\overrightarrow{EG}$=(1,1,-1).设平面EFG的法向量为$\overrightarrow{n}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=0}\\{\overrightarrow{n}•\overrightarrow{EG}=0}\end{array}\right.$,可得$\overrightarrow{n}$,利用法向量的夹角即可得出.
解答 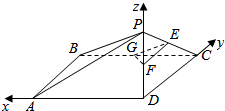 (1)证明:∵PD⊥平面ABCD,
(1)证明:∵PD⊥平面ABCD,
∴PD⊥CD,
∵CD⊥AD,PD∩AD=D.
∴CD⊥平面PAD,
∵CD?平面PCD,
∴平面PCD⊥平面PAD.
(2)解:如图以D为原点,以DA,DC,DP分别为x,y,z轴建立空间直角坐标系D-xyz.
不妨设AB=BC=$\frac{1}{2}AP$=2.则G(1,2,0),E(0,1,1),F(0,0,1),
$\overrightarrow{EF}$=(0,-1,0),$\overrightarrow{EG}$=(1,1,-1).
设平面EFG的法向量为$\overrightarrow{n}$=(x,y,z),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=0}\\{\overrightarrow{n}•\overrightarrow{EG}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{-y=0}\\{x+y-z=0}\end{array}\right.$,令x=1,解得z=1,y=0,
∴$\overrightarrow{n}$=(1,0,1)为平面PCD的一个法向量,
$\overrightarrow{DA}$=(1,0,0).
∴$cos<\overrightarrow{DA},\overrightarrow{n}>=\frac{\overrightarrow{DA}•\overrightarrow{n}}{|\overrightarrow{DA}||\overrightarrow{n}|}=\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$.
∴面GEF与面EFD所成锐二面角的大小45°.
点评 本题考查了线面面面垂直的判定与性质定理,考查了通过建立空间直角坐标系利用平面的法向量的夹角得出二面角的方法,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

( )
| A. | y=$\frac{3}{2}$x-$\frac{1}{2}$ | B. | y=2x-1 | C. | y=2x+1 | D. | y=$\frac{1}{2}$x+$\frac{1}{2}$ |
| A. | 9x-16y+7=0 | B. | 16x+9y-25=0 | C. | 9x+16y-25=0 | D. | 16x-9y-7=0 |
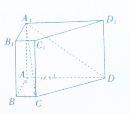 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4. 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.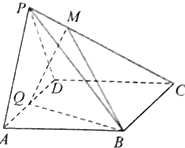 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.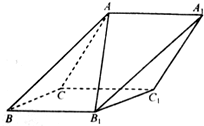 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.