题目内容
12.已知直线l的参数方程$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$ (t为参数),⊙L的极坐标方程为ρ=4sin(θ-$\frac{π}{2}$),求直线l的普通方程和⊙L的直角坐标方程.分析 利用等量代换消去t可得直线l的普通方程;利用诱导公式及极坐标与直角坐标的互化公式可得⊙L的直角坐标方程.
解答 解:由$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$ 得$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}t=-x-1}\\{\frac{1}{2}t=y-\sqrt{3}}\end{array}\right.$,
所以$-x-1=\sqrt{3}(y-\sqrt{3})$,
即直线l的普通方程为:$x+\sqrt{3}y-2=0$;
由ρ=4sin(θ-$\frac{π}{2}$)得ρ=-4cosθ,
从而ρ2=-4ρcosθ,
所以⊙L的直角坐标方程为:x2+y2+4x=0.
点评 本小题主要考查坐标系与参数方程的相关知识,具体涉及到极坐标方程、参数方程与普通方程的互化、三角变换等内容,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.曲线y=ex+3在(0,4)处的切线方程为( )
| A. | 2x+y-4=0 | B. | 2x-y+4=0 | C. | x-y+4=0 | D. | x+y-4=0 |
7.对于任意实数a,b,定义min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,定义在R上的偶函数f(x)满足f(x-4)=f(x),且当0≤x≤2时,f(x)=min{2x-1,2-x},若方程f(x)-mx=0恰有4个零点,则m的取值范围是( )
| A. | (-$\frac{1}{3}$,$\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{5}$) | C. | ($\frac{1}{5}$,$\frac{1}{3}$) | D. | (-$\frac{1}{3}$.$\frac{1}{5}$)∪($\frac{1}{5}$,$\frac{1}{3}$) |
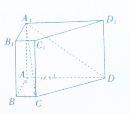 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4.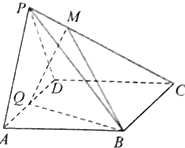 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.