题目内容
10. 如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.
如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.(1)求证:PE∥平面ABCD;
(2)求三棱锥A-BCE的体积.
分析 (1)取AD的中点M,连接MP,MB,利用三角形的中位线定理、平行四边形的判定定理可得:四边形BEPM是平行四边形,于是PE∥BM,再利用线面平行的判定定理可得:PE∥平面ABCD.
(2)在△ABC中,由余弦定理可得:AC2=AB2+BC2-2AB•BCcos∠ABC=1,因此AC2+AB2=BC2,AC⊥AB.利用面面垂直的性质定理可得:AC⊥平面ABEF,
再利用VA-BCE=VC-ABE=$\frac{1}{3}{S}_{△ABE}×AC$即可得出.
解答 (1)证明:取AD的中点M,连接MP,MB,
∵P为DF的中点,∴$MP\underset{∥}{=}\frac{1}{2}AF$,
又∵$BE\underset{∥}{=}\frac{1}{2}AF$,∴$BE\underset{∥}{=}MP$,
∴四边形BEPM是平行四边形,
∴PE∥BM,
又PE?平面ABCD,BM?平面ABCD.
∴PE∥平面ABCD.
(2)解:在△ABC中,由余弦定理可得:
AC2=AB2+BC2-2AB•BCcos∠ABC=$1+(\sqrt{2})^{2}-2×1×\sqrt{2}×cos\frac{π}{4}$=1,
∴AC=1,
∴AC2+AB2=BC2,
∴AC⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
∴AC⊥平面ABEF,
∵${S}_{△ABE}=\frac{1}{2}BE•AB$=$\frac{1}{2}×1×1$=$\frac{1}{2}$.
∴VA-BCE=VC-ABE=$\frac{1}{3}{S}_{△ABE}×AC$=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
点评 本题考查了三角形的中位线定理、平行四边形的判定定理与性质定理、线面平行的判定定理、余弦定理、面面垂直的性质定理、三棱锥的体积计算公式、勾股定理的逆定理,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 与点B的坐标相同 | |
| B. | 与点B的坐标不相同 | |
| C. | 当A与原点O重合时,与点B的坐标相同 | |
| D. | 当B与原点O重合时,与点A的坐标相同 |
 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.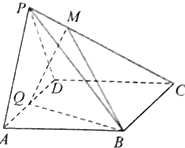 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.