题目内容
13.已知函数f(x)=x-$\frac{a}{x}$.g(x)=2ln(x+m),(Ⅰ)当m=0时,存在x0∈[$\frac{1}{e}$,e](e为自然对数的底数),使x0f(x0)≥g(x0),求实数a的取值范围;
(Ⅱ)当a=m=1时,
(1)求最大正整数n,使得对任意n+1个实数xi(i=1,2…,n+1),当xi∈[e-1,2](e为自然对数的底数)时,都有$\sum_{i=1}^{n}$f(xi)<2015g(xn+1)成立;
(2)设H(x)=xf(x)+g(x),在H(x)的图象上是否存在不同的两点A(x1,y1),B(x2,y2)(x1>x2>-1),使得H(x1)-H(x2)=H′($\frac{{x}_{1}+{x}_{2}}{2}$)(x1-x2).
分析 (I)x0f(x0)≥g(x0)可化为${x}_{0}^{2}$-a≥2lnx0,从而可得a≤${x}_{0}^{2}$-2lnx0,令h(x)=x2-2lnx,从而化简函数的最大值问题,由导数求单调性,再求最大值即可.
(II) (1)$\sum_{i=1}^{n}$f(xi)<2015g(xn+1)恒成立可化为[$\sum_{i=1}^{n}$f(xi)]max<[2015g(xn+1)]min;从而化为函数的最值问题,从而求解即可;
(2)化简H(x)=xf(x)+g(x)=x2+2ln(x+1)-1,求导H′(x)=$\frac{2}{x+1}$+2x;再化简$\frac{H({x}_{1})-H({x}_{2})}{{x}_{1}-{x}_{2}}$=$\frac{2}{{x}_{1}-{x}_{2}}$ln$\frac{{x}_{1}+1}{{x}_{2}+1}$+(x1+x2);从而可得H′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{4}{{x}_{1}+{x}_{2}+2}$+(x1+x2);即ln$\frac{{x}_{1}+1}{{x}_{2}+1}$=2$\frac{({x}_{1}+1)-({x}_{2}+1)}{({x}_{1}+1)+({x}_{2}+1)}$,令$\frac{{x}_{1}+1}{{x}_{2}+1}$=t,(t∈(1,+∞)),从而化为lnt=2(1-$\frac{2}{t+1}$),再构造函数u(t)=lnt+$\frac{4}{t+1}$-2,从而求导确定函数的单调性及取值即可.
解答 解:(I)x0f(x0)≥g(x0)可化为${x}_{0}^{2}$-a≥2lnx0,
即a≤${x}_{0}^{2}$-2lnx0,
令h(x)=x2-2lnx,
则h′(x)=2x-$\frac{2}{x}$=$\frac{2(x-1)(x+1)}{x}$,(x>0)
∴当x∈[$\frac{1}{e}$,1)时,h′(x)<0;当x∈(1,e]时,h′(x)>0;
又∵h($\frac{1}{e}$)=$\frac{1}{{e}^{2}}$+2<h(e)=e2-2,
∴hmax(x)=e2-2,
则a≤e2-2;
(II) (1)$\sum_{i=1}^{n}$f(xi)<2015g(xn+1)恒成立可化为[$\sum_{i=1}^{n}$f(xi)]max<[2015g(xn+1)]min;
∵f(x),g(x)均为增函数,
∴[$\sum_{i=1}^{n}$f(xi)]max=n(2-$\frac{1}{2}$)=$\frac{3}{2}n$,[2015g(xn+1)]min=2015×2=4030;
∴$\frac{3}{2}$n<4030,即n<2686+$\frac{2}{3}$;
∴n的最大值为2686.
(2)H(x)=xf(x)+g(x)=x2+2ln(x+1)-1,
H′(x)=$\frac{2}{x+1}$+2x;
$\frac{H({x}_{1})-H({x}_{2})}{{x}_{1}-{x}_{2}}$=$\frac{2}{{x}_{1}-{x}_{2}}$ln$\frac{{x}_{1}+1}{{x}_{2}+1}$+(x1+x2);
H′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{4}{{x}_{1}+{x}_{2}+2}$+(x1+x2);
故可化为$\frac{2}{{x}_{1}-{x}_{2}}$ln$\frac{{x}_{1}+1}{{x}_{2}+1}$=$\frac{4}{{x}_{1}+{x}_{2}+2}$,
即ln$\frac{{x}_{1}+1}{{x}_{2}+1}$=2$\frac{({x}_{1}+1)-({x}_{2}+1)}{({x}_{1}+1)+({x}_{2}+1)}$①
令$\frac{{x}_{1}+1}{{x}_{2}+1}$=t,(t∈(1,+∞)),
①式可化为lnt=2(1-$\frac{2}{t+1}$),
令u(t)=lnt+$\frac{4}{t+1}$-2,
u′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴u(t)在(1,+∞)上是增函数;
∴u(t)>u(1)=0;
∴u(t)无零点,
故A、B两点不存在.
点评 本题考查了导数的综合应用,同时考查了恒成立问题及存在性问题,属于难题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | 2x+y-4=0 | B. | 2x-y+4=0 | C. | x-y+4=0 | D. | x+y-4=0 |
| A. | 与点B的坐标相同 | |
| B. | 与点B的坐标不相同 | |
| C. | 当A与原点O重合时,与点B的坐标相同 | |
| D. | 当B与原点O重合时,与点A的坐标相同 |
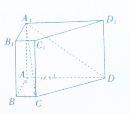 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=5,BC=1,侧棱AA1=4. 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,PA=AB,点E是PD的中点,作EF⊥PC交PC于F.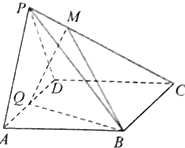 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=$\sqrt{2}$,AD=PB=2.