题目内容
20.图中.AE=$\frac{1}{4}$AC,且三角形CDE的面积是三角形ABC的一半,那么BD的长度是DC的几分之几?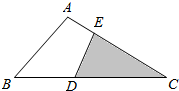
分析 直接利用三角形的面积的关系,列出方程求解即可.
解答 解:.AE=$\frac{1}{4}$AC,CE=$\frac{3}{4}$AC且三角形CDE的面积是三角形ABC的一半,
可得:$\frac{1}{2}×\frac{1}{2}CA•CBsinC=\frac{1}{2}CE•CDsinC$,
∴$\frac{2}{3}CB=CD$.BD=$\frac{1}{2}$DC.
那么BD的长度是DC的$\frac{1}{2}$.
点评 本题考查三角形的面积公式的应用,三角形边长关系,考查计算能力.

练习册系列答案
相关题目
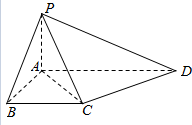 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.