题目内容
18.如果执行如图的程序框图,那么输出的m的值为$\frac{1}{3}$.
分析 模拟执行程序框图,依次写出每次循环得到的m,i的值,当i=2014时不满足条件i≤2013,退出循环,输出m的值为$\frac{1}{3}$.
解答 解:模拟执行程序框图,可得
m=$\frac{1}{2}$,i=1
m=-1,i=2
满足条件i≤2013,m=$\frac{3}{2}$,i=3
满足条件i≤2013,m=$\frac{1}{3}$,i=4
满足条件i≤2013,m=-2,i=5
满足条件i≤2013,m=$\frac{3}{2}$,i=6
满足条件i≤2013,m=$\frac{1}{3}$,i=7
满足条件i≤2013,m=-2,i=8
…
观察规律可知,m的取值以3为周期,2013=3×671,故有
满足条件i≤2013,m=$\frac{3}{2}$,i=2013
满足条件i≤2013,m=$\frac{1}{3}$,i=2014
不满足条件i≤2013,退出循环,输出m的值为$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查了循环结构的程序框图,正确写出每次循环得到的m,i的值是解题的关键,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
9.已知集合A={x|-1≤x≤1},B={x|x2-5x+6≥0},则下列结论中正确的是( )
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
6.已知数列{an}满足a1=3,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,则a2012=( )
| A. | 2 | B. | -3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
13.某校高二(9)班学生在五月月考中数学不及格的占16%,语文不及格的占7%,两门都不及格的占4%,已知该班某学生在五月月考中数学不及格,则该学生在王月月考中语文不及格的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{4}$ |
3.计算$\frac{i}{1-i}$=-( )
| A. | $\frac{-1+i}{2}$ | B. | $\frac{-1-i}{2}$ | C. | $\frac{1-i}{2}$ | D. | $\frac{1+i}{2}$ |
10.设Sn为等比数列{an}的前n项和,若8a3+a6=0,则$\frac{{S}_{6}}{{S}_{2}}$=( )
| A. | -11 | B. | -21 | C. | 11 | D. | 21 |
7. 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | B. | -$\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ |
8.若将如图的展开图还原成成正方体,则∠ABC的度数为( )
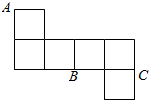

| A. | 120° | B. | 90° | C. | 60° | D. | 45° |