题目内容
设F1,F2分别是椭圆 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )| A.1 | B. | C.2 | D. |
D
试题分析:由已知得
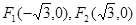 ,且设
,且设 ,则有:
,则有: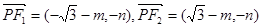 由PF1⊥PF2得
由PF1⊥PF2得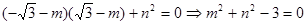 ①且
①且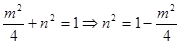 代入①得:
代入①得: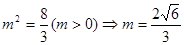 ;故选D.
;故选D.
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
题目内容
 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )| A.1 | B. | C.2 | D. |
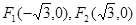 ,且设
,且设 ,则有:
,则有: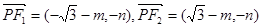 由PF1⊥PF2得
由PF1⊥PF2得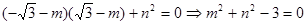 ①且
①且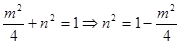 代入①得:
代入①得: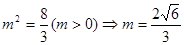 ;故选D.
;故选D.
 快捷英语周周练系列答案
快捷英语周周练系列答案