题目内容
15.若二项式(x+$\frac{a}{\root{3}{x}}$)8的展开式中x4的系数为7,则实数a=( )| A. | 2$\root{3}{6}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{\root{3}{36}}{12}$ |
分析 在二项展开式的通项公式中,令x的幂指数等于4,求出r的值,即可求得展开式中x4的系数,再根据展开式中x4的系数为7,求得a的值.
解答 解:二项式(x+$\frac{a}{\root{3}{x}}$)8的展开式的通项公式为 Tr+1=${C}_{8}^{r}$•ar•${x}^{8-\frac{4r}{3}}$,
令8-$\frac{4r}{3}$=4,求得r=3,可得展开式中x4的系数为${C}_{8}^{3}$•a3=7,a=$\frac{1}{2}$,
故选:C.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
 是
是 上的奇函数,且
上的奇函数,且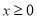 时,
时, ,则
,则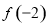 的值为____________.
的值为____________. 如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.
如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.