题目内容
【题目】设集合![]() 为函数
为函数![]() 的定义域,集合
的定义域,集合![]() 为不等式
为不等式![]() 的解集.
的解集.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
(1)利用题意首先求得集合A,B,然后求解交集可得A∩B= [1,2)
(2)首先求得![]() ,然后结合子集的定义得到关于实数a的不等式,求解不等式可得实数
,然后结合子集的定义得到关于实数a的不等式,求解不等式可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)由函数有意义得![]() ,即(1+x)(2-x)>0,
,即(1+x)(2-x)>0,
解得-1<x<2,即A={x|-1<x<2}.
解不等式(x-1)(x+2)≥0得x≤-2或x≥1,即B={x|x≤-2或x≥1}.
∴A∩B={x|1≤x<2}=[1,2).
(2)由(1)知RA={x|x≤-1或x≥2},
解不等式(ax-1)(x+2)≥0得x≤-2或x≥![]() ,即B={x|x≤-2或x≥
,即B={x|x≤-2或x≥![]() },
},
∵BRA,∴![]() ≥2,解得0<a≤
≥2,解得0<a≤![]() .
.
即实数![]() 的取值范围是
的取值范围是![]() .
.

 愉快的寒假南京出版社系列答案
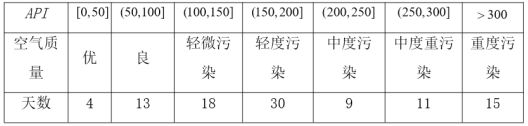
愉快的寒假南京出版社系列答案【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() 的检测数据,结果统计如下:
的检测数据,结果统计如下:
记某企业每天由空气污染造成的经济损失![]() (单位:元),空气质量指数
(单位:元),空气质量指数![]() 为
为![]() .在区间
.在区间![]() 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当![]() 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当![]() 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面![]() 列联表,并判断
列联表,并判断
能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |