题目内容
【题目】已知函数f（x）=lnx，g（x）= 
x2﹣kx；
（1）设k=m+ 
（m＞0），若函数h（x）=f（x）+g（x）在区间（0，2）内有且仅有一个极值点，求实数m的取值范围；
（2）设M（x）=f（x）﹣g（x），若函数M（x）存在两个零点x1 ， x2（x1＞x2），且满足2x0=x1+x2 ， 问：函数M（x）在（x0 ， M（x0））处的切线能否平行于直线y=1，若能，求出该切线方程，若不能，请说明理由．
【答案】
（1）解：因为h（x）=lnx+ 
x2﹣kx；
h′（x）= 
+x﹣k，
由题意可得：k≥ 
，
m+ 
=k≥ ，
可得0＜m≤ 或m≥2，
综上，m的取值范围为{m丨0＜m≤ 或m≥2}
（2）解：假设，函数M（x）在（x0，M（x0））处的切线平行于直线y=1，
M（x）=f（x）﹣g（x）=lnx﹣ x2+kx，M′（x）=f（x）﹣g（x）= ﹣x+k，
，
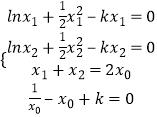由ln 
﹣ （x1+x2）（x1﹣x2）=﹣k（x1﹣x2），
∴﹣k= 
﹣x0，结合 
，
可得：ln = 
= 
，
令u= ∈（0，1），
∴lnu﹣ 
=0，u∈（0，1），
设y=lnu﹣ ，u∈（0，1），
y′= 
+ 
= 
= 
＞0，
所以函数y=lnu﹣ ，在（0，1）上单调递增，
因此，y＜0，即lnu﹣ ＜0，也就是ln ＜ ，此时与ln = 矛盾，所以数M（x）在（x0，M（x0））处的切线不能平行于直线y=1
【解析】（1）求得h（x）及h′（x），由题意可知k≥ ，及k=m+ 求得m的取值范围；（2）求得M（x）及M′（x），采用反证法，假设，函数M（x）在（x0 ， M（x0））处的切线平行于直线y=1，根据题意列出方程，求得k的解析式，构造辅助函数，利用导数求得函数的单调性及最值，判断与已知是否相符，即可验证是否存在函数M（x）在（x0 ， M（x0））处的切线平行于直线y=1，
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减，以及对函数的极值与导数的理解，了解求函数的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧,右侧
,那么
是极小值．
