题目内容
11.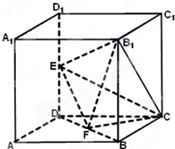 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.(Ⅰ)求证:EF∥平面ABC1D1;
(Ⅱ)求三棱锥V${\;}_{C-{B}_{1}FE}$的体积.
分析 (Ⅰ)欲证EF∥平面ABC1D1,只需在平面ABC1D1中找一直线与EF平行,根据E、F分别为DD1、DB的中点,可得EF∥BD1,最后根据线面平行的判定定理可得结论;
(Ⅱ)由题意,可先证明出CF⊥平面BDD1B1,由此得出三棱锥的高,再求出底面△B1EF的面积,然后再由棱锥的体积公式即可求得体积.
解答 (Ⅰ)证明:连接BD1,
∵E、F分别为DD1、DB的中点,
∴EF是三角形BD1D的中位线,即EF∥BD1;…(3分)
又EF?平面ABC1D1,BD1?平面ABC1D1,…(5分)
所以EF∥平面ABC1D1
(Ⅱ)解:∵EF⊥平面B1FC,∴EF⊥FB1
EF=$\sqrt{3}$,FB1=$\sqrt{6}$
Rt△B1EF的面积=$\frac{1}{2}$×EF×FB1=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{6}$=$\frac{3}{2}\sqrt{2}$
∵CB=CD,BF=DF,∴CF⊥BD.
∵DD1⊥平面ABCD,∴DD1⊥CF
又DD1∩BD=D,∴CF⊥平面BDD1B1
又CF=$\sqrt{2}$,
∴VB1-EFC=${V_{C-{B_1}EF}}=\frac{1}{3}•{S_{△{B_1}EF}}•CF=\frac{1}{3}•\frac{{3\sqrt{2}}}{2}•\sqrt{2}$=1…(12分)
点评 本题主要考查了线面平行的判定定理、线面垂直的判定定理,考查三棱锥的体积,同时考查了推理论证的能力和空间想象能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
2.如果一个复数与它的模的和为5+$\sqrt{3}$i,那么这个复数是( )
| A. | $\frac{11}{5}$ | B. | $\sqrt{3}$ | C. | $\frac{11}{5}$+$\sqrt{3}$i | D. | $\frac{11}{5}$+2$\sqrt{3}$i |
6.已知向量$\overrightarrow a=(-3,4)$,以下存在唯一实数对λ,μ使$\overrightarrow a=λ\overrightarrow{e_1}+μ\overrightarrow{e_2}$成立的一组向量$\overrightarrow{e_1},\overrightarrow{e_2}$是( )
| A. | $\overrightarrow{e_1}=(-1,2),\overrightarrow{e_2}=(3,-1)$ | B. | $\overrightarrow{e_1}=(1,3),\overrightarrow{e_2}=(2,6)$ | ||
| C. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(-1,2)$ | D. | $\overrightarrow{e_1}=(1,1),\overrightarrow{e_2}=(3,3)$ |
16.把病人送到医院看病的过程用框图表示,则此框图称为( )
| A. | 工序流程图 | B. | 程序流程图 | C. | 组织流程图 | D. | 程序步骤图 |
1.设公差不为0的等差数列{an}首项a1=9,且a4是a1与a8的等比中项,则公差d=( )
| A. | $\frac{1}{9}$ | B. | 1 | C. | 6 | D. | 9 |
 如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.
如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.