题目内容
1.若x,y满足|x|+|y|≤1,则z=$\frac{y}{x-3}$的取值范围是$[{-\frac{1}{3},\;\;\frac{1}{3}}]$.分析 作出不等式组对应的平面区域,利用斜率公式结合数形结合进行求解即可.
解答 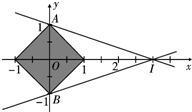 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
由$z=\frac{y}{x-3}=\frac{y-0}{x-3}$,由斜率公式可知,其几何意义是点(x,y)与点(3,0)所在直线的斜率,
故而由图可知,${z_{min}}={k_{AI}}=-\frac{1}{3}$,${z_{max}}={k_{BI}}=\frac{1}{3}$,
故而z的取值范围是$[{-\frac{1}{3},\;\;\frac{1}{3}}]$.
故答案为:$[{-\frac{1}{3},\;\;\frac{1}{3}}]$.
点评 本题主要考查线性规划和直线斜率的应用,利用数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若当r趋近于0时,$\frac{{f({x_0})-f({{x_0}+5r})}}{4r}=1$,则f′(x0)=( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $-\frac{5}{4}$ | D. | $-\frac{4}{5}$ |
10.已知$sin(π+α)=\frac{{\sqrt{3}}}{2}$,则$cos(α-\frac{3π}{2})$的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
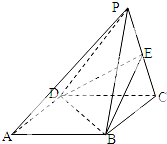 如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.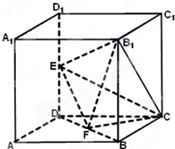 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.