题目内容
20.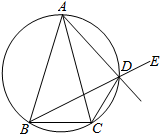 已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.
已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,△ABC中BC边上的高为1+$\frac{\sqrt{3}}{2}$,求△ABC外接圆的面积.
分析 (1)要证明AD的延长线平分∠CDE,即证明∠EDF=∠CDF,转化为证明∠ADB=∠CDF,再根据A,B,C,D四点共圆的性质,和等腰三角形角之间的关系即可得到.
(2)求△ABC外接圆的面积.只需解出圆半径,故作等腰三角形底边上的垂直平分线即过圆心,再连接OC,根据角之间的关系在三角形内即可求得圆半径,可得到外接圆面积.
解答 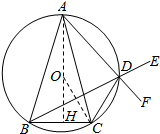 (1)证明:如图,设F为AD延长线上一点,A?B?C?D四点共圆.
(1)证明:如图,设F为AD延长线上一点,A?B?C?D四点共圆.
∴∠CDF=∠ABC,
又AB=AC,∴∠ABC=∠ACB,且∠ADB=∠ACB,
∴∠ADB=∠CDF
对顶角∠EDF=∠ADB,故∠EDF=∠CDF,
即AD的延长线平分∠CDE,…(4分)
(2)解:设O为外接圆圆心,连接AO比延长交BC于H,交⊙O于点M,连接OC,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴AH⊥BC.
∴∠OAC=∠OAB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×30°=15°,
∴∠COH=2∠OAC=30°,
设圆半径为r,
则OH=OC•cos30°=$\frac{\sqrt{3}}{2}$r,
∵△ABC中BC边上的高为1+$\frac{\sqrt{3}}{2}$,
∴AH=OA+OH=r+$\frac{\sqrt{3}}{2}$r=1+$\frac{\sqrt{3}}{2}$,
解得:r=1,
∴△ABC的外接圆的面积为:π(10分)
点评 此题主要考查圆内接多边形的性质、圆周角定理、等腰三角形的性质以及三角形的外接圆的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
10.过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若|AB|=$\frac{25}{12}$,|AF|<|BF|,则|AF|为( )
| A. | 1 | B. | $\frac{5}{6}$ | C. | 2 | D. | $\frac{4}{3}$ |
12.函数$f(x)=\sqrt{1-{{log}_2}(x-1)}$的定义域为( )
| A. | (1,3] | B. | (-∞,3] | C. | (0,3] | D. | (1,3) |
9.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=$\frac{π}{3}$,记椭圆和双曲线的离心率分别为e1,e2,则$\frac{1}{{e}_{1}{e}_{2}}$的最大值为( )
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径. 如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.
如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论. 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.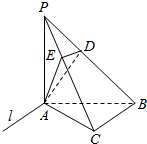 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.