题目内容
14.某校高-年级举行语、数、英三科竞赛.高一(2)班共有32名同学参加三科竞赛.有16人参加语文竞赛,有10人参加数学竞赛,有16人参加英语竞赛,同时 参加语文竞赛和数学竞赛的有3人.同时参加语文竞赛和英语竞赛的有3人.没有人同时参加全部三科竞赛.问:同时参加数学竞赛和英语竞赛的有多少人?只参加语文竞赛的有多少人?分析 设只参加语文竞赛的有x人,只参加数学竞赛的有y人,只参加英语竞赛的有z人,同时参加数学竞赛和英语竞赛的有p人,结合已知画出满足条件的图形,数形结合构造方程组,解得答案.
解答 解:如下图所示:
设只参加语文竞赛的有x人,只参加数学竞赛的有y人,只参加英语竞赛的有z人,
同时参加数学竞赛和英语竞赛的有p人,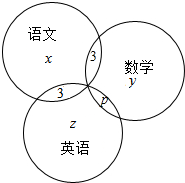
则有:x+y+z+p+3+3=32,
x+3+3=16,
y+p+3=10,
z+p+3=16,
解得:x=10,p=4,
即同时参加数学竞赛和英语竞赛的有4人,只参加语文竞赛的有10人.
点评 本题考查的知识点是Venn图表达集合的关系及运算,根据已知画出满足条件的图形,数形结合构造方程组,是解答的关键.

练习册系列答案
相关题目