Question

【题目】如图，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C．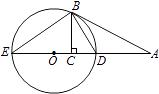

（1）证明：∠CBD=∠DBA；
（2）若AD=3DC，BC= ，求⊙O的直径．

Answer 1

【答案】
（1）证明：∵DE是⊙O的直径，

则∠BED+∠EDB=90°，

∵BC⊥DE，

∴∠CBD+∠EDB=90°，即∠CBD=∠BED，

∵AB切⊙O于点B，

∴∠DBA=∠BED，即∠CBD=∠DBA；

（2）证明：由（1）知BD平分∠CBA，

则 =3，

∵BC= ，

∴AB=3 ，AC= =4，

则AD=3，

由切割线定理得AB2=ADAE，

即AE= ，

故DE=AE﹣AD=3，

即可⊙O的直径为3．

【解析】（1）根据直径的性质即可证明：∠CBD=∠DBA；（2）结合割线定理进行求解即可求⊙O的直径．