题目内容
【题目】设正数![]() 、
、![]() 满足
满足![]() 会且使得关于
会且使得关于![]() 的不等式
的不等式![]() 总有实数解.试求
总有实数解.试求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】
首先,求出![]() 、
、![]() 应满足的条件.由原不等式得下列的各个等价形式:
应满足的条件.由原不等式得下列的各个等价形式:![]() ,两边同时平方并整理得
,两边同时平方并整理得![]() . ①
. ①
令![]() ,则
,则![]() ,代入式①得
,代入式①得
![]() ,
,
即![]() . ②
. ②
下面分3种情形讨论:
当![]() 时,式②变为
时,式②变为![]() ,有解.
,有解.
当![]() ,
,![]() 充分大时
充分大时![]() ,式②有解.
,式②有解.
当![]() 时,首先要求判别式
时,首先要求判别式![]() ,有
,有![]() ,
,
即![]() . ③
. ③
令![]() .
.
由于![]() ,所以,方程
,所以,方程![]() 有两个实根
有两个实根![]() 、
、![]() .因为
.因为![]() ,所以,必有
,所以,必有![]() .又因为抛物线
.又因为抛物线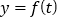 开口向上,所以,不等式
开口向上,所以,不等式![]() 在
在![]() 时总是有解
时总是有解![]() .
.
综合上述得,![]() 、
、![]() 应满足的充分必要条件是
应满足的充分必要条件是![]() , ④
, ④
即![]() . ⑤
. ⑤
注意到式⑤与三角恒等式![]() 的“相似性”,
的“相似性”,
故令![]() ,
,![]() .
.
则![]()
![]() ,
,
其中![]() ,
,![]() .
.
令![]() ,则
,则![]() . ⑥
. ⑥
当![]() 时,由式⑥得
时,由式⑥得![]() ,
,![]() .
.
当![]() 时,由式⑥解得
时,由式⑥解得![]()
![]() .
.
若![]() ,则
,则![]() ,
,
即![]()
它等价于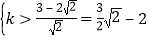
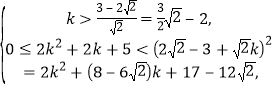
即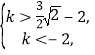 矛盾.
矛盾.
故这种情形不可能存在.从而,只有一种可能,
即![]() .
.
于是,![]() .
.
这时有两种可能:
(1)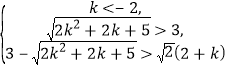
或(2)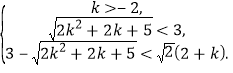
由(1)可解得![]() ,由(2)可解得
,由(2)可解得![]() .
.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.
又![]() ,所以,
,所以,![]() 的取值范围是
的取值范围是![]() ,即
,即![]() 能取遍
能取遍![]() 中的每一个值(
中的每一个值(![]() 与
与![]() 是相互独立的).
是相互独立的).

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了![]() 名员工进行问卷调查,其中
名员工进行问卷调查,其中![]() 的员工工作积极.经汇总调查,这
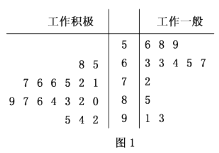
的员工工作积极.经汇总调查,这![]() 名员工是否支持企业改革的调查得分(百分制)如茎叶图(图
名员工是否支持企业改革的调查得分(百分制)如茎叶图(图![]() )所示.调查评价标准指出:调查得分不低于
)所示.调查评价标准指出:调查得分不低于![]() 分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
(1)根据以上资料完成下面的![]() 列联表,结合数据能否有
列联表,结合数据能否有![]() 的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
积极支持企业改革 | 不太赞成企业改革 | 总计 | |
工作积极 | |||
工作一般 | |||
总计 |
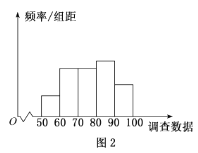
(2)现将![]() 名员工的调查得分分为如下
名员工的调查得分分为如下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 其频率分布直方图如图
其频率分布直方图如图![]() 所示,这
所示,这![]() 名员工的调查数据得分的平均值可由茎叶图得到,记为
名员工的调查数据得分的平均值可由茎叶图得到,记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),
(同一组中的数据用该组区间的中点值作代表),![]() 与
与![]() 的误差值在
的误差值在![]() 以内,可以由
以内,可以由![]() 代替
代替![]() ,能否由
,能否由![]() 代替
代替![]() ?(提示:
?(提示:![]() 名员工的调查数据得分的和
名员工的调查数据得分的和![]() )
)
(3)该企业人力资源部从![]() 分以上的员工中任选
分以上的员工中任选![]() 名员工进行座谈,则所选员工的分数超过
名员工进行座谈,则所选员工的分数超过![]() 分的人数的数学期望是多少?
分的人数的数学期望是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: .
.
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
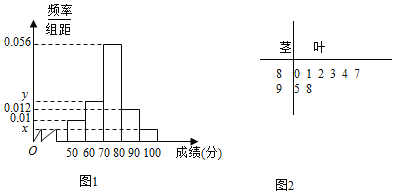
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.