题目内容
【题目】如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1 ， ∠BAA1=60°．
（Ⅰ）证明AB⊥A1C；
（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB，求直线A1C与平面BB1C1C所成角的正弦值．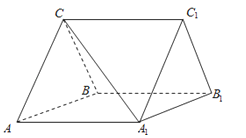
【答案】解：（Ⅰ）取AB的中点O，连接OC，OA1 ， A1B，
因为CA=CB，所以OC⊥AB，由于AB=AA1 ， ∠BAA1=60°，
所以△AA1B为等边三角形，所以OA1⊥AB，
又因为OC∩OA1=O，所以AB⊥平面OA1C，
又A1C平面OA1C，故AB⊥A1C；
（Ⅱ）由（Ⅰ）知OC⊥AB，OA1⊥AB，又平面ABC⊥平面AA1B1B，交线为AB，
所以OC⊥平面AA1B1B，故OA，OA1 ， OC两两垂直．
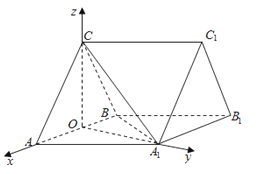
以O为坐标原点，
的方向为x轴的正向，||为单位长，建立如图所示的坐标系，
可得A（1，0，0），A1（0，
，0），C（0，0，），B（﹣1，0，0），
则
=（1，0，），
=
=（﹣1，，0），
=（0，﹣，），
设
=（x，y，z）为平面BB1C1C的法向量，则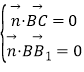
，即
，
可取y=1，可得=（，1，﹣1），故cos＜，＞=
=-
，
又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值，
故直线A1C与平面BB1C1C所成角的正弦值为：．
【解析】（Ⅰ）取AB的中点O，连接OC，OAspan>1 ， A1B，由已知可证OA1⊥AB，AB⊥平面OA1C，进而可得AB⊥A1C；
（Ⅱ）易证OA，OA1 ， OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立坐标系，可得 ， ， 的坐标，设=（x，y，z）为平面BB1C1C的法向量，则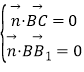 ， 可解得=（ ， 1，﹣1），可求|cos＜ ， ＞|，即为所求正弦值．
【考点精析】关于本题考查的直线与平面垂直的性质，需要了解垂直于同一个平面的两条直线平行才能得出正确答案．
