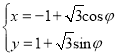��Ŀ����
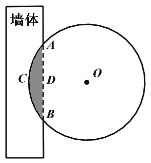
����Ŀ�����������������ҹ��Ŵ�������ѧ���䣬���жԹ��ɶ�������������������һǧ���꣬����������һ�����⣺������Բ�����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ�������Ϊ������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ��ò��ϣ������1�磬�����1�ߣ������Բ����ľ�ϵ�ֱ���Ƕ��٣���Ϊ0.5�ɵ�Բ����ľ�IJ�����Ƕ��ǽ���У�����ͼ��ͼ��ʾ����Ӱ����Ϊ��Ƕ��ǽ���ڵIJ��֣�.��֪��![]() �ߣ����θ�
�ߣ����θ�![]() �磬�����ľ����Ƕǽ�ڲ��ֵ����ԼΪ�� ����ע��һ��=10��=100�磬
�磬�����ľ����Ƕǽ�ڲ��ֵ����ԼΪ�� ����ע��һ��=10��=100�磬![]() ��
��
A.300������B.305.6������C.310������D.316.6������
���𰸡�D
��������
�������ͼ����Ӱ���ֵ��������������������ʽ����ľ����Ƕǽ�ڲ��ֵ����.
�����ͼ��Բ�İ뾶Ϊ![]() ���磩����
���磩����![]() �����
�����![]() .
.
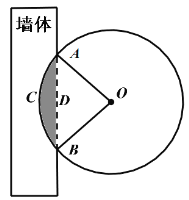
��ͼ���ڽ���ͼ������![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��![]() .
.
��Ӱ���ֵ����ԼΪ![]() ��
��
��ľ����Ƕǽ�ڲ��ֵ����ԼΪ![]() �������磩��
�������磩��
��ѡ��D.

����Ŀ������������㷢����ǰ�ҹ�����������Ч�ļ��㹤�ߣ�Ϊ�ҹ��Ŵ���ѧ�ķ�չ�����˺ܴ���.�����������У��ԡ���ʽ���͡���ʽ�����ַ�ʽ����ʾ���֣����±���
������ʽ |
|
|
|
|
|
|
|
|
|
��ʽ |
|
|
|
|
|
|
|
|
|
��ʽ |
|
|
|
|
|
|
|
|
|
��ʾ��λ��ʱ����λ����ʽ��ʮλ�ú�ʽ����λ����ʽ��ǧλ�ú�ʽ���Դ����ƣ��������ÿգ���ͼ��ʾ.�����![]() ��������ʵ��ķ�ʽȫ����������ı����У���ô���Ա�ʾ����λ���ĸ���Ϊ______.
��������ʵ��ķ�ʽȫ����������ı����У���ô���Ա�ʾ����λ���ĸ���Ϊ______.
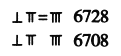
����Ŀ��ij��ѧij����Ϊ�о�����ѧ������������ѧʱ������ѧ�����еĽ����÷ֵĹ�ϵ�����������ij��ѧ����ij��![]() ��ѧ��ÿ�ܿ���������ѧʱ��
��ѧ��ÿ�ܿ���������ѧʱ��![]() (��λ��Сʱ)�������ѧ�����п�����ѧ�����÷�
(��λ��Сʱ)�������ѧ�����п�����ѧ�����÷�![]() ���������±���
���������±���
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
��1�������������ݣ������ѧ�����еĽ����÷�![]() ���ѧ������������ѧʱ��
���ѧ������������ѧʱ��![]() �����Իع鷽�̣���Ԥ��ijѧ��ÿ�ܿ���������ѧʱ��Ϊ
�����Իع鷽�̣���Ԥ��ijѧ��ÿ�ܿ���������ѧʱ��Ϊ![]() Сʱ����ѧ�����еĽ����÷֣�
Сʱ����ѧ�����еĽ����÷֣�
��2������![]() ������ѡ
������ѡ![]() �ˣ���
�ˣ���![]() ����������
����������![]() �˿���������ѧʱ�䲻����
�˿���������ѧʱ�䲻����![]() Сʱ�ĸ���.
Сʱ�ĸ���.
�ο���ʽ��![]() ������
������ ��
��![]() ���ο����ݣ�
���ο����ݣ�![]()