题目内容
【题目】小明同学对棱长为2的正方体的性质进行研究，得到了如下结论：①12条棱中可构成16对异面直线；②过正方体的一个顶点的截面可能是三角形、四边形、五边形、六边形；③以正方体各表面中心为顶点的正八面体的表面积是
；④与正方体各棱相切的球的体积是：
.其中正确的序号是______.
【答案】④
【解析】
画出图形，对四个选项逐一分析即可得出正确选项.
对于①，12条棱中可构成异面直线的有24对，原因为：对于每一条棱，有三条和它平行，四条和它相交，因此有4条和他是异面，而扩展到12条棱为：
，而由于两条作为一对，需要再除以2，得到24对，故错误；
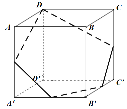
对于②，如下图，过正方体的一个顶点的截面可能是三角形、四边形、五边形，故错误；
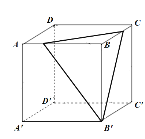
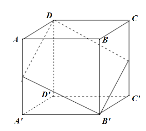
对于③，先画出图形：
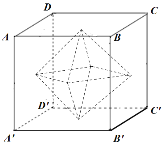
正八面体每个面是全等的正三角形，棱长为
，表面积为
，故错误；
对于④，由于此球与正方体的各棱相切，则球的半径正好是正方体的面对角线的一半，
正方体的棱长为2，则球的半径是
，则
，故正确.
故答案为：④.
练习册系列答案
相关题目
