Question

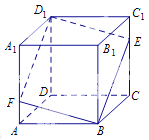
【题目】袋中共有8个球，其中有3个白球，5个黑球，这些球除颜色外完全相同．从袋中随机取出一球，如果取出白球，则把它放回袋中；如果取出黑球，则该黑球不再放回，并且另补一个白球放入袋中．重复上述过程次后，袋中白球的个数记为．

（1）求随机变量的概率分布及数学期望；

（2）求随机变量的数学期望关于的表达式．

Answer 1

【答案】（1）概率分布详见解析，；（2）．

【解析】

（1）的可能取值为3，4，5，计算概率得到分布列，计算数学期望得到答案.

（2）设，则，计算概率得到数学期望，整理化简得到，根据数列知识得到答案.

（1）由题意可知3，4，5．

当时，即二次摸球均摸到白球，其概率是；

当时，即二次摸球恰好摸到一白，一黑球，

其概率是；

当时，即二次摸球均摸到黑球，其概率是，

所以随机变量的概率分布如下表：

数学期望.

（2）设，0，1，2，3，4，5．

则，．

，，，

，，

，

∴

，

由此可知，，

又，故是首项为，公比为的等比数列，

∴，即.