题目内容
【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系,随机调查了某中学高三某班![]() 名学生每周课下钻研数学时间
名学生每周课下钻研数学时间![]() (单位:小时)与高三下学期期中考试数学解答题得分
(单位:小时)与高三下学期期中考试数学解答题得分![]() ,数据如下表:
,数据如下表:
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
(1)根据上述数据,求出数学考试中的解答题得分![]() 与该学生课下钻研数学时间
与该学生课下钻研数学时间![]() 的线性回归方程,并预测某学生每周课下钻研数学时间为
的线性回归方程,并预测某学生每周课下钻研数学时间为![]() 小时其数学考试中的解答题得分;
小时其数学考试中的解答题得分;
(2)从这![]() 人中任选
人中任选![]() 人,求
人,求![]() 人中至少有
人中至少有![]() 人课下钻研数学时间不低于
人课下钻研数学时间不低于![]() 小时的概率.
小时的概率.
参考公式:![]() ,其中
,其中 ,
,![]() ;参考数据:
;参考数据:![]()
【答案】(1)线性回归方程: ![]() ,预测值为:
,预测值为:![]() 分(2)
分(2)![]()
【解析】
(1)先求均值,再代入公式求![]() ,即得线性回归方程;在线性回归方程令
,即得线性回归方程;在线性回归方程令![]() ,解得预测值;
,解得预测值;
(2)利用枚举法确定总基本事件数以及所求事件包含的基本事件数,最后根据古典概型概率公式求结果.
(1)![]()
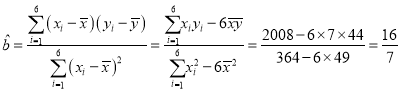
![]()
![]()
当![]() 时,
时,![]()
预测值为:![]() 分
分
(2)设“这2人中至少有一个人刻下钻研数学时间不低于8小时为事件A”
所有基本事件如下:
(2,4),(2,6),(2,8),(2,10),(2,12),(4,6),(4,8),(4,10),(4,12), (6,8),(6,10),(6,12),(8,10),(8,12),(10,12)
共15个基本事件
事件A包含(2,8),(2,10),(2,12),(4,8),(4,10),(4,12),(6,8),(6,10)(6,12),(8,10),(8,12),(10,12)共12个基本事件
所以![]()

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目