题目内容
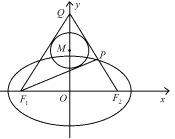
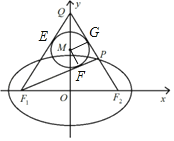
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 点为圆
点为圆![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设内切圆与三角形各边的切点,再由直角三角形![]() 中,由勾股定理可得椭圆的
中,由勾股定理可得椭圆的![]() 值,再由
值,再由![]() 可得
可得![]() 的值,由
的值,由![]() ,
,![]() ,
,![]() 之间的关系求出椭圆的方程;
之间的关系求出椭圆的方程;
(2)由(1)得直线![]() 的方程,由圆心到直线的距离为半径1,求出圆
的方程,由圆心到直线的距离为半径1,求出圆![]() 的圆心坐标,可得圆的方程,设
的圆心坐标,可得圆的方程,设![]() 的参数坐标,可得数量积的表达式,进而求出其取值范围.
的参数坐标,可得数量积的表达式,进而求出其取值范围.
解:(1)设![]() 的内切圆
的内切圆![]() 切
切![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 连接
连接![]() ,
,![]() ,
,
因为![]() ,因为
,因为![]() ,所以四边形
,所以四边形![]() 为正方形,所以
为正方形,所以![]() ,
,
设![]() ,
,![]() ,由
,由![]() ,且
,且![]() ,有
,有![]() ,则
,则![]() ,
,![]() ,
,
由![]() 得
得![]()
![]() ,有
,有![]() ,
,
故![]() ,即
,即![]() ,
,![]() ,
,
所以椭圆的方程的标准方程:![]() ;
;
(2)设点![]() ,其到直线
,其到直线![]() 的距离为1,
的距离为1,
有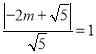 ,解得
,解得![]() 或
或![]() (舍),即
(舍),即![]() .
.
故圆![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
由![]() ,
,![]() ,
,
所以![]() ,
,![]()
有![]()
![]()
因为![]()
所以![]()
故![]() 为
为![]() .
.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】干支历法是上古文明的产物,又称节气历或中国阳历,是一部深奥的历法.它是用60组各不相同的天干地支标记年月日时的历法.具体的算法如下:先用年份的尾数查出天干,如2013年3为癸;再用2013年除以12余数为9,9为巳.那么2013年就是癸巳年了,
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | ||
4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | |||
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 |
2020年高三应届毕业生李东是壬午年出生,李东的父亲比他大25岁.问李东的父亲是哪一年出生( )
A.甲子B.乙丑C.丁巳D.丙卯