Question

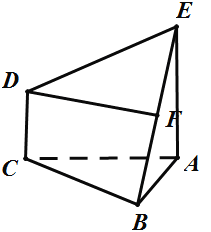
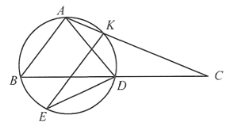
【题目】如图所示，D是△ABC中，边BC的中点，K为AC与△ABD的外接圆O的交点，EK平行于AB且与圆O交于E，若AD=DE，求证：.

Answer 1

【答案】证明见解析

【解析】

如图所示，连结DK并延长，与BA的延长线交于点P，连结AE，

由AD=DE，得.

由EK∥AB，得∠EKD=∠BPD，

又，

所以∠BPD=∠AKP，故AK=AP.

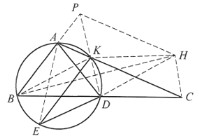
作PH∥AC，并使PH=PB，连结HK、BK、BH、DH，

在△PBK与△PHK中，.

由PH∥AC可得，

所以△PBk≌△PHK，故BK=HK.

又由PB=PH，得PD是线段BH的垂直平分线，即有PD⊥BH，.

由D是BC的中点，得DC=BD=DH，所以BH⊥HC，故DK∥HC.

再由PH∥KC，得四边形PKCH为平行四边形，

所以，即AB+AK=KC.