题目内容
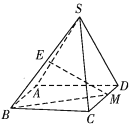
【题目】在如图所示的几何体ABCDE中，
平面ABC，
，
，F是线段AD的中点，
.
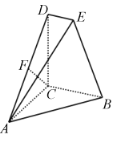
（1）求证：
；
（2）若
，求三棱锥
的体积.
【答案】（1）证明见解析；（2）
【解析】
（1）求出CF⊥AD，AE⊥CF，从而CF⊥平面ADE，进而CF⊥DE，由DE∥BC，得CF⊥CB，由DC⊥平面ABC，DC⊥BC，从而BC⊥平面ACD，由此能证明AC⊥BC．
（2）由CA⊥CD，CA⊥CB，DE∥BC，得B，C，D，E四点共面，从而CA⊥平面BDE，由此能求出三棱锥F-ABE的体积．
证明：(1)∵
，F是线段AD的中点，∴
.
又
，
，∴
平面ADE，
∴
，又
，∴
，
∵
平面ABC，∴
，
又∵
，∴
平面ACD，
∵
平面ACD，∴
.
(2)∵
，
，
，
又∵，
∴B，C，D，E四点共面，
∴
平面BDE，
∵
，F为线段AD的中点
∴
.
练习册系列答案
相关题目
