题目内容
12.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|=5,向量$\overrightarrow{c}$-$\overrightarrow{a}$,$\overrightarrow{c}$-$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,|$\overrightarrow{c}$-$\overrightarrow{a}$|=2$\sqrt{3}$,则$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{c}$-$\overrightarrow{b}$的夹角正弦值为$\frac{3}{5}$,|$\overrightarrow{c}$|=4+$\sqrt{3}$或$\sqrt{37-16\sqrt{3}}$.分析 作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,向量$\overrightarrow{c}$-$\overrightarrow{a}$=$\overrightarrow{AC}$,$\overrightarrow{c}$-$\overrightarrow{b}$=$\overrightarrow{BC}$,运用四点共圆的知识和解三角形的正弦、余弦定理,即可得到所求.
解答 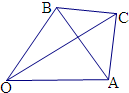 解:作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
解:作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
则$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,向量$\overrightarrow{c}$-$\overrightarrow{a}$=$\overrightarrow{AC}$,$\overrightarrow{c}$-$\overrightarrow{b}$=$\overrightarrow{BC}$,
由题意可得△OAB为边长为5的等边三角形,
向量$\overrightarrow{c}$-$\overrightarrow{a}$,$\overrightarrow{c}$-$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,可得∠ACB=120°,
由∠AOB+∠ACB=180°,可得四点O,A,B,C共圆,
在△ABC中,CA=2$\sqrt{3}$,AB=5,∠ACB=120°,
由正弦定理可得sin∠CBA=$\frac{AC•sin120°}{AB}$=$\frac{2\sqrt{3}•\frac{\sqrt{3}}{2}}{5}$=$\frac{3}{5}$,
在△OAC中,OA=5,AC=2$\sqrt{3}$,∠OCA=60°,
由余弦定理可得52=OC2+12-2OC•2$\sqrt{3}$•$\frac{1}{2}$,
解得OC=4+$\sqrt{3}$.
当C在△OAB中,同理可得sin∠CBA=$\frac{3}{5}$,OC=$\sqrt{37-16\sqrt{3}}$.
故答案为:$\frac{3}{5}$,4+$\sqrt{3}$或$\sqrt{37-16\sqrt{3}}$.
点评 本题考查向量的三角形法则和向量夹角的概念,同时考查解三角形的正弦、余弦定理的运用,考查运算能力,属于中档题.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | 非奇非偶函数 | B. | 既奇又偶函数 | C. | 奇函数 | D. | 偶函数 |
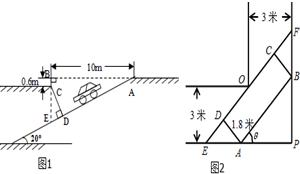 随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.
随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图. 如图,已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,试用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$.
如图,已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,试用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$.