��Ŀ����
17��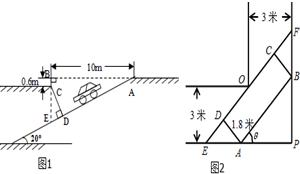 ����˽�ҳ��������࣬����С����ͣ���ѡ���������ͻ��������ij����С��Ϊ���⡰ͣ���ѡ����⣬�⽨�����ͣ���⣬�������ʦ�ṩ�˸õ���ͣ�������ںͽ�����ֱ��ת�䴦��ƽ�����ʾ��ͼ��
����˽�ҳ��������࣬����С����ͣ���ѡ���������ͻ��������ij����С��Ϊ���⡰ͣ���ѡ����⣬�⽨�����ͣ���⣬�������ʦ�ṩ�˸õ���ͣ�������ںͽ�����ֱ��ת�䴦��ƽ�����ʾ��ͼ����1�����涨������ͣ�����µ����Ϸ�Ҫ�����߱�־���Ա��֪ͣ���˳����ܷ�ȫʻ�룬Ϊ�����ߣ�������ݸ�ͼ1ʾ���ݼ������߶�CD��ֵ������ȷ��0.1m��
�����������ṩ�ο���sin20��=0.3420��cos20��=0.9397��tan20��=0.3640��
��2���ڳ�������һ��ֱ�ǹ��䳵����������ƽ��ͼ��ͼ2ʾ�����PAB=�ȣ�rad����������Ϊ3�ף�����һ��ת������С��������ˮƽ����ͼΪ���Σ����Ŀ�Ϊ1.8�ף���Ϊ4.5�ף��ʴ˳��Ƿ���˳��ͨ����ֱ�ǹ��䳵����
���� ��1����Rt��ABE�У����BE��ֵ���ٵó�CE��ֵ�������CD���ɣ�
��2������ͼ�Σ�������Ǻ��������ʣ���ʾ��EF��DE��AB�ij�������AB����Сֵ�����ж�С�����Ƿ���ͨ��ֱ�������
��� �⣺��1���ڡ�ABE�У���ABE=90�㣬��BAE=20�㣬
��tan��BAE=$\frac{BE}{AB}$��
��AB=10��
��BE=AB•tan��BAE=10tan20���3.6m��
��BC=0.6����CE=BE-BC=3m��
�ڡ�CED�У���CD��AE����ECD=��BAE=20�㣬
��cos��ECD=$\frac{CD}{CE}$����CD=CE•cos��ECD=3cos20���3��0.94��2.8m��
�ʴ�Ϊ2.8m��
��2���ӳ�CD��ֱ�����ȵı��ཻ��E��F��
��EF=OE+OF=$\frac{3}{cos��}$+$\frac{3}{sin��}$������0���ȣ�$\frac{��}{2}$��
��DE=$\frac{1.8}{tan��}$��
CF=BC•tan��=1.8tan�ȣ�
�֡�AB=DC=EF-��DE+CF����
��f���ȣ�=$\frac{3}{cos��}$+$\frac{3}{sin��}$-1.8��tan��+$\frac{1}{tan��}$��
=$\frac{��sin��+cos�ȣ�-1.8}{sin��cos��}$������0���ȣ�$\frac{��}{2}$��
��sin��+cos��=t����t=$\sqrt{2}$sin����+$\frac{��}{4}$����
��1��t��$\sqrt{2}$
��sin��cos��=$\frac{{t}^{2}-1}{2}$��
��f���ȣ�=g��t��=$\frac{6t-3.6}{{t}^{2}-1}$��
��g�䣨t��=-$\frac{6��t-0.6��^{2}+3.84}{��{t}^{2}-1��^{2}}$��
�֡�1��t��$\sqrt{2}$��
��g�䣨t����0�������
��g��t��=$\frac{6t-3.6}{{t}^{2}-1}$��t�ʣ�1��$\sqrt{2}$]���Ǽ�������
��g��t��min=g��$\sqrt{2}$��=6$\sqrt{2}$-3.6��4.5��
��С�����ܹ�˳��ͨ��ֱ�ǹ��䳵����
���� ���⿼�������Ǻ�����ͼ�������ʵ�Ӧ�����⣬Ҳ�����˽������ε�Ӧ�����⣬���ۺ�����Ŀ��

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ģ��1�����ָ��2Ϊ0.97�� | B�� | ģ��2�����ָ��R2Ϊ0.89�� | ||
| C�� | ģ��3�����ָ��R2Ϊ0.56 �� | D�� | ģ��4�����ָ��R2Ϊ0.45�� |