题目内容
4.设点(a,b)是区域$\left\{\begin{array}{l}{x+y-4≤0}\\{x>0,y>0}\end{array}\right.$内的随机点,函数f(x)=ax2-4bx+1在区间[1,+∞)上是增函数的概率为$\frac{1}{3}$.分析 求出不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{x>0,y>0}\end{array}\right.$表示的平面区域图形的面积,再求出f(x)在区间[1,+∞)上是增函数时满足的条件所表示的平面区域面积,利用几何概型的概率公式求出概率即可.
解答 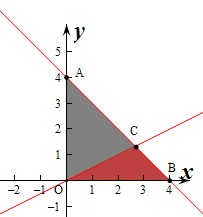 解:作出不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{x>0,y>0}\end{array}\right.$表示的平面区域如图所示,
解:作出不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{x>0,y>0}\end{array}\right.$表示的平面区域如图所示,
对应的图形为△OAB,其中对应面积为S△OAB=$\frac{1}{2}$×4×4=8,
若f(x)=ax2-4bx+1在区间[1,+∞)上是增函数,
则满足a>0且对称轴x=-$\frac{-4b}{2a}$=$\frac{2b}{a}$≤1,
即$\left\{\begin{array}{l}{a>0}\\{a≥2b}\end{array}\right.$,对应的平面区域为△OBC,
由$\left\{\begin{array}{l}{a=2b}\\{a+b-4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{8}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴对应的面积为S△OBC=$\frac{1}{2}$×4×$\frac{4}{3}$=$\frac{8}{3}$,
∴根据几何概型的概率公式可知所求的概率为P=$\frac{\frac{8}{3}}{8}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了二元一次不等式组表示平面区域的应用问题,也考查了几何概型的应用问题,是基础题目.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | k≤2 | B. | -1<k<0 | C. | -2≤k<-1 | D. | k≤-2 |
| A. | 模型1(相关指数2为0.97) | B. | 模型2(相关指数R2为0.89) | ||
| C. | 模型3(相关指数R2为0.56 ) | D. | 模型4(相关指数R2为0.45) |