题目内容
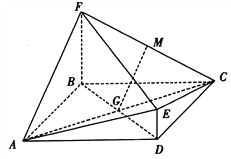
【题目】如图,菱![]() 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, ![]() .
.
(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1) 取![]() 的中点
的中点![]() ,连接
,连接![]() .由
.由![]() ,又因为
,又因为![]() ,且
,且![]() ,所以平面
,所以平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;(2) 连接
;(2) 连接![]() ,由
,由![]() .设菱形的边长为2,则
.设菱形的边长为2,则![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,得
,得![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() ,
, ![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
试题解析:证明:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() 为菱形对角线的交点,所以
为菱形对角线的交点,所以![]() 为
为![]() 中点,所以
中点,所以![]() ,又因为
,又因为![]() 分别为
分别为
![]() 的中点,所以
的中点,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
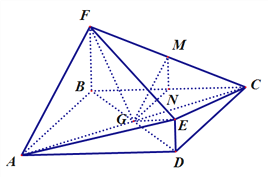
(Ⅱ)证明:连接![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形,
所以![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() .
.
设菱形的边长为2, ![]() ,
,
则![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
则![]() ,
, ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,得
,得![]() 平面
平面![]() ,
,
在直角三角形![]() 中,
中, ![]() ,
,
又在直角梯形![]() 中,得
中,得![]() ,
,
从而![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
点睛:直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行,即线线平行推出线面平行.两平面垂直的判定有两种方法:(1)两个平面所成的二面角是直角;(2)一个平面经过另一平面的垂线.掌握基本的判定和性质定理外还应理解线线、线面、面面垂直的转化思想,逐步学会综合运用数学知识分析解决问题的能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
