题目内容
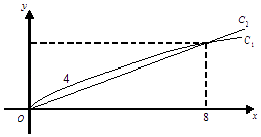
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
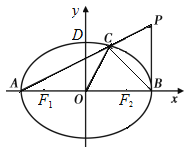
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C.
,连接PA交椭圆于点C.
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求t的最小值.

【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1) 由题意![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ,又
,又![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的弦长为
相交得到的弦长为![]() ,则
,则![]() 进而可得椭圆
进而可得椭圆![]() 的方程.(2) 设直线
的方程.(2) 设直线![]() 的方程为
的方程为![]() ,联立直线PA和椭圆方程,可得点
,联立直线PA和椭圆方程,可得点![]() 的坐标是
的坐标是![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() ,
, ![]()
![]() ,所以
,所以![]() .将线段BC,OP的长度用t来表示,则
.将线段BC,OP的长度用t来表示,则 ![]() ,
, ![]() ,所以
,所以![]() ,整理得
,整理得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() .
.
试题解析:(Ⅰ)因为以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,所以
,所以![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ,
,
又![]() ,所以
,所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的
相交得到的
弦长为![]() ,则
,则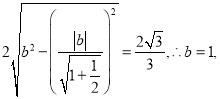 所以
所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由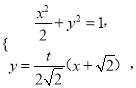
整理得![]() ,
,
解得: ![]() ,
, ![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,由于直线
,由于直线![]() 的斜率为
的斜率为![]() ,
,
所以![]()
![]() ,所以
,所以![]() .
.
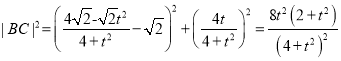 ,
, ![]() ,
,
所以![]() ,
,
![]() ,所以
,所以![]() ,
,
整理得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00﹣22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有99%的把握认为“在20:00﹣22:00时间段居民的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X.求X的数学期望和方差.
P(X2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
附:X2= ![]() .
.