题目内容
过抛物线 = 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
= 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
A.相交 B.相离 C.相切 D.不能确定
 = 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
= 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )A.相交 B.相离 C.相切 D.不能确定
C
专题:综合题.
分析:设P为AB中点,A、B、P在准线l上射影分别为M、N、Q,根据抛物线的定义,可知AP+BP=AM+BN,从而 PQ=
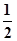 AB,所以以AB为直径作圆则此圆与准线l相切.
AB,所以以AB为直径作圆则此圆与准线l相切.解答:解:设AB为过抛物线焦点F的弦,P为AB中点,A、B、P在准线l上射影分别为M、N、Q,
∵AP+BP=AM+BN
∴PQ=
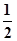 AB,
AB,∴以AB为直径作圆则此圆与准线l相切
故选C.
点评:本题以抛物线为载体,考查抛物线过焦点弦的性质,关键是正确运用抛物线的定义,合理转化,综合性强.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 ,过曲线
,过曲线 上 一点
上 一点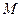 的切线
的切线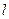 ,与曲线
,与曲线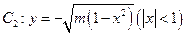 也相切于点
也相切于点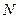 ,记点
,记点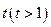 。
。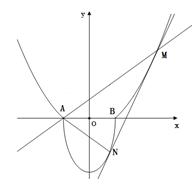
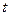 表示
表示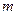 的值和点
的值和点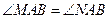 ?
?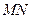 所在直线的方程。
所在直线的方程。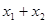 =6,那么
=6,那么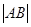 = ( *** )
= ( *** ) 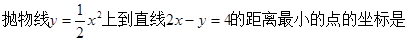 ( )
( )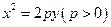 上一点M到焦点的距离是
上一点M到焦点的距离是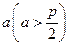 ,则点M的纵坐标是
,则点M的纵坐标是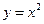 和直线
和直线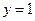 所围成图形的面积为______________
所围成图形的面积为______________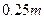 ,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到
,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到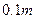 )
)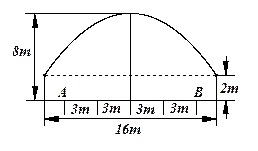
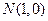 ,动点
,动点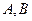
 分别在抛物线
分别在抛物线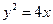 及曲线
及曲线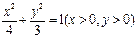 上,若
上,若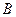 在
在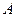 的右侧,且
的右侧,且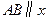 轴,则
轴,则
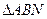 的周长
的周长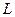 的取值范围是
的取值范围是 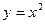 上的点,若过点P的切线方程与直线
上的点,若过点P的切线方程与直线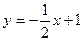 垂直,则过P点处的切线方程是____________.
垂直,则过P点处的切线方程是____________.