题目内容
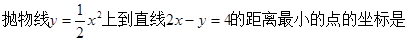 ( )
( )| A.(1,1) | B.(1,2) | C.(2,2) | D.(2,4) |
C
分析:先设直线y=2x+t是抛物线的切线,最小距离是两直线之间的距离,于抛物线方程联立消去y,再根据判别式等于0求得t,代入方程求得x,进而求得y,答案可得.
解答:解:设直线y=2x+t是抛物线的切线,最小距离是两直线之间的距离,
代入化简得x2-4x-2t=0
由△=0得t=-2
代入方程得x=2,y=2
∴P为(2,2)
故选C.
解答:解:设直线y=2x+t是抛物线的切线,最小距离是两直线之间的距离,
代入化简得x2-4x-2t=0
由△=0得t=-2
代入方程得x=2,y=2
∴P为(2,2)
故选C.

练习册系列答案
相关题目
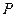 的轨迹
的轨迹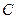 的方程为
的方程为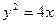 ,过焦点
,过焦点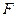 的直线
的直线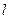 与
与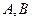 两点,
两点,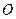 为坐标原点。(1)求
为坐标原点。(1)求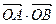 的值;
的值;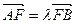 ,当三角形
,当三角形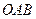 的面积
的面积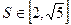 时,求
时,求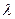 的取值范围.
的取值范围. = 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
= 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )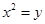 的准线方程是(***)
的准线方程是(***)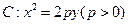 截得的弦长为
截得的弦长为 。
。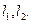
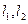 交于点M,求直线AB的方程;
交于点M,求直线AB的方程;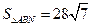 时,求点N的坐标
时,求点N的坐标 上任意两点(直线AB不垂直于
上任意两点(直线AB不垂直于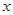 轴),线段AB的中垂线交
轴),线段AB的中垂线交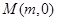 ,则
,则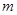 的取值范围是_______
的取值范围是_______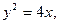 焦点为F,
焦点为F,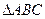 三个顶点均在抛物线上,若
三个顶点均在抛物线上,若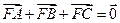 则|FA|+|FB|+|FC|= 。
则|FA|+|FB|+|FC|= 。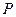 是抛物线
是抛物线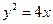 上一动点,则点
上一动点,则点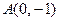 的距离与
的距离与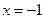 的距离和
的距离和 的最小值是( )
的最小值是( )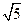

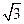
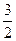
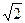
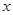 轴上的抛物线被直线
轴上的抛物线被直线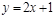 截得的弦长为
截得的弦长为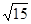 ,求抛物线的方程。
,求抛物线的方程。