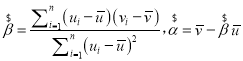题目内容
【题目】已知实数a、b满足a2+b2-ab＝3．
（1）求a-b的取值范围；
（2）若ab＞0，求证：
．
【答案】（1）﹣2≤a﹣b≤2；（2）证明见解析．
【解析】
（1）由已知得a2+b2＝3+ab≥2|ab|．
①当ab≥0时，3+ab≥2ab，解得ab≤3，即0≤ab≤3；
②当ab＜0时，3+ab≥﹣2ab，解得 ab≥﹣1，即﹣1≤ab＜0，
得0≤3﹣ab≤4，即0≤（a﹣b）2≤4，即﹣2≤a﹣b≤2；
（2）由（1）知0＜ab≤3，可得
，
利用配方法即可容易证明.
（1）因为a2+b2﹣ab＝3，所以a2+b2＝3+ab≥2|ab|．
①当ab≥0时，3+ab≥2ab，解得ab≤3，即0≤ab≤3；
②当ab＜0时，3+ab≥﹣2ab，解得 ab≥﹣1，即﹣1≤ab＜0，
所以﹣1≤ab≤3，则0≤3﹣ab≤4，
而（a﹣b）2＝a2+b2﹣2ab＝3+ab﹣2ab＝3﹣ab，
所以0≤（a﹣b）2≤4，即﹣2≤a﹣b≤2；
（2）由（1）知0＜ab≤3，
因为
当且仅当ab＝2时取等号，
所以
．
练习册系列答案
相关题目
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示，绘制相应的散点图，如图所示：
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量（万只） | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |
根据表及图得到以下判断：①羊只数量与草场植被指数成减函数关系；②若利用这五组数据得到的两变量间的相关系数为
，去掉第一年数据后得到的相关系数为
，则
；③可以利用回归直线方程，准确地得到当羊只数量为2万只时的草场植被指数；以上判断中正确的个数是（ ）
A.0B.1C.2D.3
